Regressão Ridge e Lasso

Regressão linear é o primeiro algoritmo que aprendemos quando estudamos ciência de dados e machine learning. Apesar de muito útil, o algoritmo buscará sempre minimizar a soma dos quadrados de forma que se obtenha um modelo com o menor erro possível. Isso pode levar ao problema de overfitting (já explicado em posts como Overfitting e Cross Validation e Explicando overfitting com uma anedota). Uma forma de resolver isso é utilizando a regressão ridge ou lasso!

O TRADEOFF VIÉS X VARIÂNCIA

Como explicado no primeiro parágrafo, é comum nos depararmos com o problema de overfitting quando utilizamos regressão linear. Uma forma de resolver esse problema é através do que chamamos de regularização. Posto de forma simples, a regularização criará penalidades ao seu modelo de forma que você reduza a variância e aumente o viés.

Sim, soa estranho falar de aumentar o viés, mas é isso mesmo. Um bom modelo precisa ser capaz de prever dados novos. Por este motivo, existe o que chamamos de tradeoff de viés e variância (bias x variance tradeoff). Um modelo com muita variância acertará muito os dados no treino, mas errará dados novos. Já um modelo com muito viés acaba sendo um modelo super-simplificado e com baixa acurácia. Em outras palavras, há um equilíbrio entre viés e variância que queremos atingir. O modelo não pode nem ser muito simples, alto viés, nem muito complexo, alta variância.

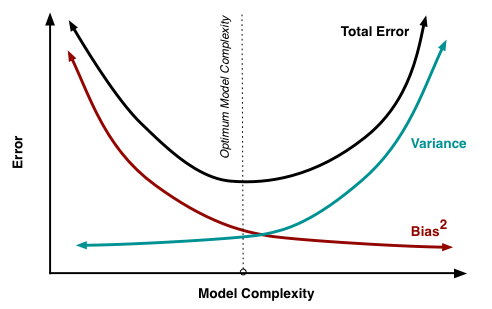
No caso da regressão linear, nosso modelo está tentando reduzir ao máximo o viés, de forma que no gráfico acima, ele estaria situado à direita. Uma forma de trazermos ele mais para a esquerda do gráfico reduzindo sua complexidade, seria através da regularização.

Resumindo, hoje você vai aprender uma forma de lidar com modelos que sofrem de overfitting. Isso normalmente ocorre por conta de multicolinearidade ou ausença de dados suficientes (número de regressores >= número de indivíduos).

REGULARIZAÇÃO L1

A primeira regularização de que vamos falar é a L1, grave bem este número e associe-o à Regressão Lasso. Neste caso, o que o modelo fará será reduzir alguns dos coeficientes da equação, podendo chegar a zero.

Quando falamos de Regressão Lasso estamos tratando de uma regressão semelhante à linear, só que aqui o que ocorre é a minimização da soma dos resíduos quadrados somados a uma constante lambda multiplicada pela soma dos coeficientes em módulo. A fórmula abaixo ilustra essa definição:

Na regressão Lasso, alguns coeficientes podem ser reduzidos a zero. Dessa forma, ela também pode ser utilizada para redução de dimensionalidade.

Outra coisa importante para se ter em mente é o lambda da equação. Este fator controla o tamanho da penalidade, sendo que pode ser:

• Igual a zero, não tendo nenhum parâmetro eliminado. Ou seja, temos o mesmo resultado que uma regressão linear;
• Maior que zero, aumentando o número de coeficientes eliminados. Em outras palavras, lambda será determinante para a complexidade do modelo. Quanto mais alto, maior o viés e menor a variância. Em outras palavras, um lambda muito baixo pode levar ao overfitting.

Mas como saber qual lambda utilizar?

Não há uma resposta certa. No caso de você estar utilizando um software de programação, você pode testar vários lambdas e avaliar o quanto o seu modelo está overfittando e quão pior fica a predição da base teste. Leia sobre RandomSearchCV, GridSearchCV e BayesSearcCV se estiver utilizando Python (bibliotecas Scikit-Learn e Scikit-Opt). No caso de R, funções parecidas são encontradas no pacote Caret.

REGULARIZAÇÃO L2

Se com L1 estamos reduzindo alguns coeficientes a zero, quando falamos de L2, eles podem no máximo chegarem próximos a zero, mas nunca vão se tornar zero. Essa é a principal diferença. E se antes estávamos tratando de regressão Lasso, agora migramos para regressão Ridge.

Primeiramente, note que a regressão Lasso pode ser útil quando temos muitas variáveis e queremos eliminar as menos importantes; porém, quando falamos de regressão ridge, temos regressões com muitas variáveis importantes. Queremos tornar nosso modelo mais simples reduzindo a magnitude dos regressores, mas não eliminar nenhum.

A regressão Ridge, tal como a Lasso, é uma variação da Regressão Linear. Dessa vez, queremos minimizar a soma dos resíduos quadrados somada a lambda multiplicado pela soma dos coeficientes ao quadrado. A fórmula abaixo ilustra o que acabamos de dizer:

Mais uma vez, a escolha de lambda determina a complexidade de seu modelo. Novamente, quanto maior lambda, mais “simples” seria nossa equação no sentido de que tiramos um pouco do efeito dos coeficientes. Então guarde bem: quanto maior o lambda, menor a variância e maior a chance de underfitting. Quanto menor lambda, maior a variância e maior chance de overfitting.

CONCLUSÃO

Ambas regressões são interessantes principalmente quando temos muitas variáveis, como quando temos mais variáveis do que indivíduos no dataset. A Regressão Lasso possui ainda a vantagem de reduzir coeficientes a zero, podendo ser uma alternativa para redução de dimensionalidade. Qual utilizar no seu problema vai depender do tipo de solução que você precisa. Mas tenha em mente que regularização é um tema relevante que todo cientista de dados precisa conhecer.

 

E aí? Gostou do conteúdo? Se inscreva para receber todas as novidades. Deixe seu e-mail em INSCREVA-SE na barra à direita, logo abaixo de pesquisar. E, por favor, não deixe de comentar, dar seu feedback e, principalmente, compartilhar com seus amigos. De verdade, isso faz toda a diferença. Além disso, você também pode acompanhar mais do meu trabalho seguindo a conta de Twitter @UniDosDados, no Instagram @universidadedosdados ou por alguma das redes que você encontra em Sobre o Estatsite / Contato, como meu canal de Youtube Canal Universidade dos Dados.

Aproveite e adquira sua camiseta de data science na LOJA DA UNIVERSIDADE DOS DADOS. Vai ficar estiloso e me ajudar neste projeto!

BONS ESTUDOS!