Análise Bidimensonal para Variáveis Quantitativas

Análise bidimensional (ou bivariada) é a análise de duas variáveis em conjunto. Quando utilizamos medidas resumo como média, mediana e variância (como no post Estatística Descritiva), estamos analisando a variável de forma isolada. Porém, em muitos casos, é interessante entender como as variáveis interagem entre si.

Por exemplo, vamos supor que você quer acompanhar o movimento do preço de uma ação de acordo com as alterações que o preço de uma outra ação. É provável que a primeira coisa que você faça seja plotar um gráfico contendo os pontos que representam os preços das duas ações em momentos diferentes. Abaixo um exemplo de um gráfico de dispersão (scatterplot) com os dados de fechamento de duas ações acompanhados ao longo do tempo:

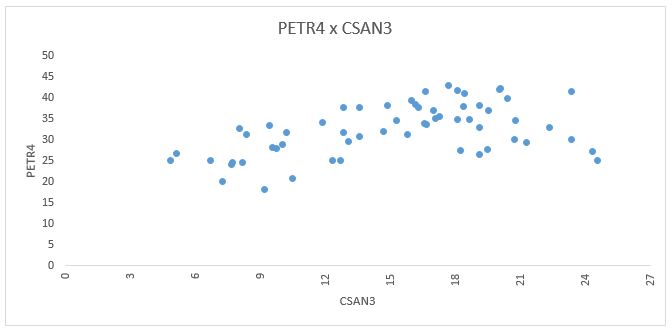
Vemos pelo nosso gráfico que as duas variáveis parecem ter uma pequena relação linear. Não está muito claro que o aumento do valor de uma se relaciona com o aumento de outra, mas parece existir algo. Como podemos ser mais precisos?

A correlação entre duas variáveis é uma forma mais precisa de se medir como elas se relacionam. Mais especificamente, o chamado coeficiente de Pearson, mede a intensidade e o sentido dessa relação. Em outras palavras, esse coeficiente é capaz de indicar se os movimentos dos preços das ações são muito próximos, quando há um movimento em um dos preços, o outro também irá oscilar. E também indicará o sentido da relação, ou seja, se o preço de uma ação subir, o preço da outra pode subir ou descer.

O valor do coeficiente de Pearson vai de -1 até 1, sendo que:

1. Coeficiente próximo de -1: Indica que as variáveis tem correlação negativa. Ou seja, quando o preço de uma sobe, o preço da outra cai.
2. Coeficiente próximo de +1: Indica que as variáveis tem correlação positiva. Ou seja, quando o preço de uma sobe, o preço da outra sobe também. E quando o preço de uma cai, o preço da outra cai também.
3. Coeficiente próximo de 0: Indica que as variáveis não são dependentes linearmente uma da outra. Ou seja, oscilação no preço de uma não indica qualquer oscilação no preço da outra.

Lembre-se que isso não quer dizer que exista causalidade. Ou seja, embora o preço das duas ações variem conjuntamente, não quer dizer que o aumento de uma implica necessariamente no aumento da outra. Isso deve ser investigado com mais cautela.

No nosso caso, o coeficiente é de 0,49. Há uma correlação moderada.

Há diversas formas de se interpretar o coeficiente como sendo forte ou fraco. Eu particularmente gosto dos intervalos abaixo retirados do Wikipedia:

• 0.9 para mais ou para menos indica uma correlação muito forte.
• 0.7 a 0.9 positivo ou negativo indica uma correlação forte.
• 0.5 a 0.7 positivo ou negativo indica uma correlação moderada.
• 0.3 a 0.5 positivo ou negativo indica uma correlação fraca.
• 0 a 0.3 positivo ou negativo indica uma correlação desprezível.

Para calcular a correlação, existe a função CORREL() no Excel e a função cor() no R.

Veja graficamente outros exemplos de correlação:

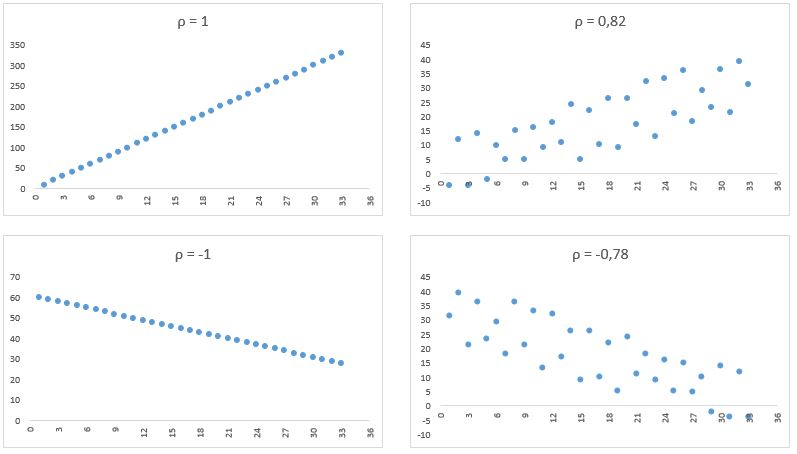
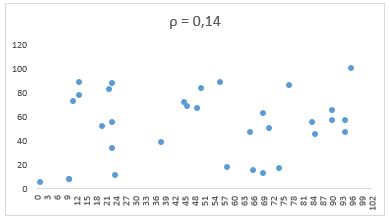
Veja que quando mais próximo de zero o coeficiente, menor é a relação linear entre as duas variáveis!

Essas são as duas formas mais básicas e essenciais para qualquer análise bidimensional. Embora pareça  algo leviano, esse tipo de análise é amplamente utilizado e traz resultados importantes em diversas áreas de estudos.

Dê uma olhada também em: Gráficos em R e Estatística Descritiva.