Testes de Hipóteses

INTRODUÇÃO: A QUESTÃO A SER RESPONDIDA

No mundo real é quase sempre impossível analisar uma população inteira para fazer um estudo. Um laboratório não conseguirá testar seu remédio em todos os indivíduos da população. O que é de praxe, é obter uma amostra, fazer os devidos testes com ela e tentar concluir se o remédio funciona ou não. Em suma, o que estamos fazendo é testando uma hipótese, a de que o remédio funciona. Mas e se você tivesse 50 pacientes e observasse que o remédio funciona para 30 deles? Isso é suficiente para concluir que o remédio funciona? Ou deveríamos concluir que ele não funciona?

É aí que entra o teste de hipóteses. Este teste consiste em testar matematicamente alguma afirmativa com base no tamanho da amostra analisada e nas medidas da população. Por exemplo, suponha que você saiba que um adulto consome em média 4.000kcal por dia, com um desvio padrão de 300kcal. Sua empresa criou um remédio para inibir a fome nos adultos. Vocês testam o remédio em 100 pacientes e verificam que a média de kcal consumidas por eles é de 3.400 após o uso do medicamento. Agora, vocês vão querer testar a hipótese de que o remédio tem efeito. Ou se a redução não é significativa o suficiente para afirmar isso.

O teste de hipóteses, pode ser resumido em 3 passos:

1. Definir suas hipóteses;
2. Calcular a probabilidade;
3. Definir o critério para tomada de decisão;

Os passos 2 e 3 podem ser invertidos. É provável que você já saiba qual vai ser o critério para tomada de decisão, mas vou deixar na ordem acima para que você entenda no passo 2 alguns cálculos e termos que serão mencionados no passo 3.

PASSO A PASSO DO TESTE DE HIPÓTESES

1. Definir suas hipóteses

Quando se realiza um teste de hipóteses é preciso definir a hipótese nula. Esta será a hipótese ‘padrão’ que será testada. Podemos dizer que é a hipótese que nos dará a resposta, ao aceitá-la ou rejeitá-la. No nosso exemplo, a hipótese nula pode ser: o consumo médio de kcal de quem toma o remédio é igual 4.000. Ou seja, é igual ao de quem não toma o remédio. Em contrapartida, precisamos definir uma hipótese alternativa, que será a hipótese que fará oposição à hipótese nula. No nosso exemplo, a hipótese alternativa é que o consumo de quem toma remédio é menor que o de quem não toma.

Note que o teste de hipóteses pode ser direcional ou não direcional. Em nosso exemplo, vamos testamos que a média de consumo não tem diferença e que a hipótese nula era a de que quem tomava o remédio consumia menos. No entanto, não haveria problema em elaborar questões em que a hipótese nula era a de que o consumo de quem tomava remédio era diferente. É possível ter uma hipótese nula em que testamos igualdade e uma hipótese alternativa que teste que há diferença. A escolha depende do seu interesse e de alguma crença prévia. Para o laboratório, se o remédio aumentar o consumo, isso já não nos interessa. O que ele quer é garantir que o remédio diminua o apetite. Caso isso não ocorra, o remédio já será descartado. Isso nos leva a dois tipos de testes:

• Teste Unicaudal (one tail test): Teste para verificar se os desvios em uma direção. Neste teste, nossa hipótese nula é de que o valor observado é maior (ou menor) que o valor de referência. Este foi o que utilizamos em nosso teste acima.
• Teste Bicaudal (two tail test): Teste para verificar desvios em qualquer direção. Este é utilizado quando você não sabe se o efeito esperado é para mais ou para menos. Seria o caso de usarmos como hipótese alternativa: os pacientes que tomam remédio consomem uma quantidade de kcal diferente da população – podendo ser para mais ou para menos.

Agora já temos nossa hipótese nula, nossa hipótese alternativa e sabemos que se trata de um teste unicaudal. Escrevemos então nossas hipóteses:

H0: μ = 4.000
H1: μ < 4.000

2. Calcular a probabilidade

Agora que você já sabe o que quer testar, é hora de calcular o z-valor e o p-valor. O z-valor é uma estatística para medir quantos desvios padrões uma observação está do parâmetro da população. Por exemplo, se a média de consumo da população é 4.000kcal com desvio padrão de 300kcal, e você tem um indivíduo que consome 3.400kcal, esse indivíduo possui um Z igual a 2, dois desvios padrão maior que a média. Cada z-valor é associado a um p-valor, ou seja, uma probabilidade (veja na tabela z).

Como calcular o z-valor?

z = (x-μ)/σ

Onde x é o ponto da curva, a observação; μ é a média da população e σ é o desvio padrão.

Parece intuitivo certo? Veja que você está calculando a diferença da sua observação para a média e o quanto ela representa do desvio padrão da população. Sério, olhe para a fórmula 100x se for preciso, para mim foi uma virada de jogo sacar isso.

Esse método funciona para distribuições normais:

 

 

 

 

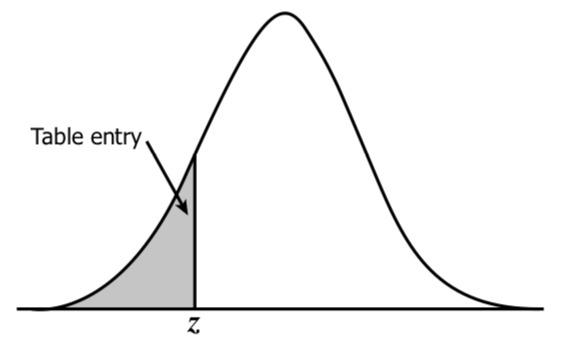
Fonte: http://users.stat.ufl.edu/~athienit/Tables/Ztable.pdf

Então, recapitulando até aqui: defina seu teste de hipóteses, i.e., escolha o que você quer testar, se a média é igual, diferente, menor ou maior; calcule o z-valor e encontre o p-valor correspondente dele. Novamente, o z-valor é uma medida de desvio padrão, você o calcula para saber o quanto o valor observado está afastado da média da população.

Um gráfico mais legal que você pode carregar contigo enquanto estuda a matéria é o seguinte:

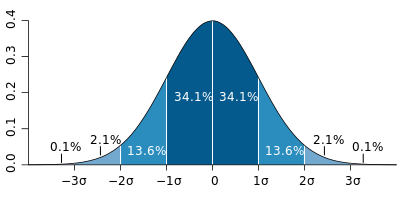
Fonte: https://www.monolitonimbus.com.br/distribuicao-normal/

Nele, é possível observar a probabilidade atrelada para cada posição em que a observação se situar.

Agora, uma dúvida que pode estar pegando aí: quem garante que minha distribuição é normal?

Para isso, nós nos baseamos no Teorema Central do Limite, que diz que a distribuição das médias das amostras se aproxima de uma normal na medida que a amostra fica maior. O quão maior? Consideramos para n > 30. Mas preste atenção no que estamos dizendo: a distribuição amostral das médias.

Vamos calcular o z-valor para nosso exercício:

z = (3400-4000)/300 = -600/300 = -2

Veja no gráfico acima que este valor cai a esquerda da curva. Sem olharmos para a tabela z, podemos verificar que a probabilidade de obtermos um valor menor ou igual a esse é de 2,2%. Sendo mais precisos, ao olharmos para a tabela z, vemos que o p-valor associado é 0,0228. Quase 2,3%. Mas e agora, temos alguma diferença estatisticamente significante entre os que tomaram o remédio e os que não tomaram? Vamos ao passo 3!

3. Definir o critério para tomada de decisão

Esse passo consiste em escolher o nível de significância. Em estatística, o nível de significância α é um valor previamente definido que servirá para definir a rejeição ou não da hipótese nula. Quando obtemos um p-valor abaixo de α no nosso teste de hipóteses, nós rejeitamos a hipótese nula. A escolha desse valor é um pouco subjetiva e ,via de regra, você vai observar que é comumente aceito α = 0,05. Ou seja, caso a gente obtenha um p-valor < 0,05, podemos rejeitar a hipótese nula. Acima disso, nós não podemos rejeitar a hipótese nula. Esse é o modo correto de interpretar os resultados, ainda que seja comum dizer que se aceita a hipótese alternativa.

Olhando para nosso experimento e para os cálculos feitos anteriormente, temos que nosso p-valor é menor que 5%. Logo, podemos rejeitar a hipótese nula com 5% de significância. Note que se o autor for mais rigoroso e utilizar um nível de significância de 1%, ele não conseguiria rejeitar a hipótese nula e assumiria que o remédio não teve um efeito na população. Utilizando 5% de significância, conseguimos rejeitar a hipótese nula de que os pacientes tratados consomem o mesmo que os pacientes não tratados. Ou seja, o remédio é eficaz.

Note que, por se tratar de probabilidade, não temos uma 100% de certeza se o remédio é ou não eficaz. Sendo assim, podemos cometer dois erros:

• Erro Tipo I (Falso Positivo): Rejeitar a hipótese nula, sendo que ela é verdadeira. Ou seja, rejeitamos a hipótese de que o remédio não tem efeito, quando na verdade ele tem;
• Erro Tipo II (Falso Negativo): Falhar em rejeitar a hipótese nula, quando na verdade ela é falsa. Ou seja, falhamos em rejeitar a hipótese de que o remédio não tem efeito, quando na verdade ele realmente não funciona.

O erro a ser assumido deve ser considerado em cada tipo de problema. Quando temos um nível de significância muito baixo, estamos sendo mais rígidos na rejeição da hipótese nula. Ou seja, aumentamos o erro tipo II. Caso a gente queira ser mais tolerante com o erro tipo I, reduzimos nosso α. Em um exame de alguma doença grave, por exemplo, a preocupação com o falso positivo talvez seja melhor do que um paciente obter um falso negativo e acabar atrasando o tratamento. Logo, é um caso onde o erro tipo I é mais aceito. Novamente, isso vai variar de problema a problema.

Acredito que isso seja o suficiente para você entender o teste de hipóteses e sua importância. Espero que realmente tenha aproveitado o post. Como é uma matéria complicada e fundamental para TUDO que vemos em estatística, seja uma modelagem mais complexa ou mesmo um experimento controlado dos mais simples, vou colocar vários exercícios para o leitor praticar.

Se tiver dúvidas, críticas ou sugestões, fique à vontade para comentar ou me escrever.

Fontes:

https://support.minitab.com/pt-br/minitab/18/help-and-how-to/statistics/basic-statistics/supporting-topics/tests-of-means/what-is-a-z-value/

https://en.wikipedia.org/wiki/Null_hypothesis#Tailedness_of_the_null-hypothesis_test

http://www.statisticshowto.com/probability-and-statistics/normal-distributions/central-limit-theorem-definition-examples/

Your Guide to Master Hypothesis Testing in Statistics

Bussab e Morettin, Estatística Básica 6ª edição