Localizando Outliers Através do Intervalo Interquartil (+ Boxplot + Código SAS)

Recentemente, estava trabalhando com uma base de mais ou menos 500 mil linhas, onde a maior parte dos dados de uma determinada variável estava no intervalo de 0 a 1.000. Esta mesma variável, no entanto, possuía algumas linhas em que o valor dela era 5.000, 10.000 e até 15.000. Ou seja, haviam alguns outliers. Isto era um problema, principalmente, quando eu construía um gráfico de distribuição. Para lidar com isso, eu exclui os outliers com base no conceito do intervalo interquartil.

O intervalo interquartil é uma medida de dispersão utilizada em estatística descritiva. Seu cálculo é simples, é a subtração do 3° quartil pelo 1° quartil (Percentil – Conceito e Código SAS). Ou seja, IQR = Q3-Q1. Essa medida é comumente utilizada na construção de boxplots (veja o último gráfico de MAIS GRÁFICOS NO R: QQPLOT()). Porém, aqui vamos utilizá-la na identificação de outliers.

A identificação de outliers – i.e., valores atípicos, distantes dos demais pontos da série – pode ser feita utilizando o IQR. Entende-se como outlier, valores menores que Q1-1,5*IQR ou valores maiores que Q3+1,5*IQR. Estes valores também são representados no boxplot, mas como pontos acima ou abaixo da linha conectada à caixa. Vejamos um desenho de um boxplot com todos estes conceitos:

Note que o boxplot é constituído de uma caixa, cuja dimensão representa o IQR. O mínimo no desenho é a representação de Q1-1,5*IQR e o máximo a de Q3+1,5*IQR. Quaisquer pontos abaixo do mínimo ou acima do máximo é considerado um outlier. Exatamente o conceito explicado no parágrafo anterior.

Agora que sabemos como identificar outliers, podemos fazer isto no SAS. Porém, o SAS não tem uma função específica para exclusão de outliers. A forma mais simples que eu encontrei, divide-se em 3 partes: (1) localizar o 1° e o 3° quartil com o proc means e salvar em uma tabela, (2) trazer os valores dos quartis para a base que está sendo trabalhada, (3) marcar quais pontos estão abaixo de Q1-1,5*IQR e acima Q3+1,5*IQR.

Primeiro, vamos gerar uma base de exemplo para trabalharmos (utilizaremos o exemplo do post Tutorial: PROC MEANS no SAS com algumas pequenas modificações):

DATA EXEMPLO;
    INPUT ID $ ESTADO $ SEXO $ FORMA_PAGTO $ VLR_COMPRA IDADE;

    CARDS;
AA123 SP M DINHEIRO 10000 22
BB001 MG F CREDITO 35500 32
AA010 BA M DEBITO 2000 35
AA003 BA F CREDITO 15 25
AA004 SP F CREDITO 1 30
AA006 SP F DINHEIRO 1500 20
BB002 BA F CREDITO 900 29
CC333 BA F DEBITO 400 25
DD444 BA M DINHEIRO 300 50
EE441 MG F CREDITO 150 30
EE332 SP F CREDITO 1000 22
EE114 BA F DINHEIRO 5000 33
EE123 MG F CREDITO 4000 60
EE456 PE M CREDITO 1500 33
AA009 BA M CREDITO 1500 65
AA111 PE F DINHEIRO 5000 19
PP154 GO F CREDITO 5000 18
PP888 GO F CREDITO 500 29
DD009 BA M CREDITO 1500 19
DD111 PE F DINHEIRO 1500 18
EF154 GO F CREDITO 1000 17
DD888 GO F CREDITO 1900 18
;
RUN;

Agora, calculamos os quartis e guardamos em uma tabela chamada quartil:

PROC MEANS DATA = EXEMPLO Q1 Q3 ;
VAR VLR_COMPRA;
OUTPUT OUT =QUARTIL 
Q1 = QUARTIL1 Q3 =QUARTIL3 ;
RUN;

Agora, precisamos trazer os valores da tabela QUARTIL para nossa tabela EXEMPLO. Isso pode ser feito com um proc sql bem simples. No exemplo abaixo, criamos a tabela EXEMPLO_2 com todos os elementos que estão na tabela EXEMPLO e com os campos QUARTIL1 e QUARTIL3 da tabela QUARTIL – se tiver alguma dificuldade com o proc sql, veja o post Tutorial: Proc Sql (SAS):

PROC SQL ;
CREATE TABLE EXEMPLO_2 AS
SELECT A. *, B.QUARTIL1, B.QUARTIL3
FROM EXEMPLO AS A,
QUARTIL AS B
;
RUN;

Agora, você tem a tabela exemplo original acrescida de duas colunas contendo o valor dos quartis. Para o último passo, vamos criar uma marcação chamada FL_OUTLIER que receberá 1 para o caso do valor de compra do cliente ser um outlier e 0 caso contrário:

DATA EXEMPLO_3;
SET EXEMPLO_2;
IF VLR_COMPRA < QUARTIL1-1.5*(QUARTIL3-QUARTIL1) THEN FL_OUTLIER = 1;
ELSE IF VLR_COMPRA > QUARTIL3+1.5*(QUARTIL3-QUARTIL1) THEN FL_OUTLIER = 1;
ELSE FL_OUTLIER = 0;
RUN;

Como toda programação, há ainda outras formas que essa marcação poderia ter sido feita. Você poderia ter feito o condicional acima em uma só linha, utilizando o OR. Você também poderia criar mais uma coluna e chamá-la de IQRinf e IQRsup, referindo-se ao intervalo interquartil inferior e superior, respectivamente. Enfim, são várias opções.

Para fazer um boxplot de uma variável no SAS, é preciso fazer uma pequena gambiarra. O PROC BOXPLOT lida com o cruzamento de variáveis. Sua sintaxe é basicamente a seguinte:

TITLE 'BOX PLOT';
PROC BOXPLOT DATA= BASE DE DADOS;
PLOT VARIAVEL_1*VARIAVEL_2;
RUN;

Como nós queremos apenas a distribuição da variável VLR_COMPRA, vamos criar uma variável qualquer que seja igual em todas as linhas e a utilizaremos como se fosse a variável 2:

DATA EXEMPLO_4;
    SET EXEMPLO_3;
    GRUPO = "A";
RUN;

TITLE 'BOX PLOT';
PROC BOXPLOT DATA=EXEMPLO_4;
PLOT VLR_COMPRA*GRUPO;
RUN;

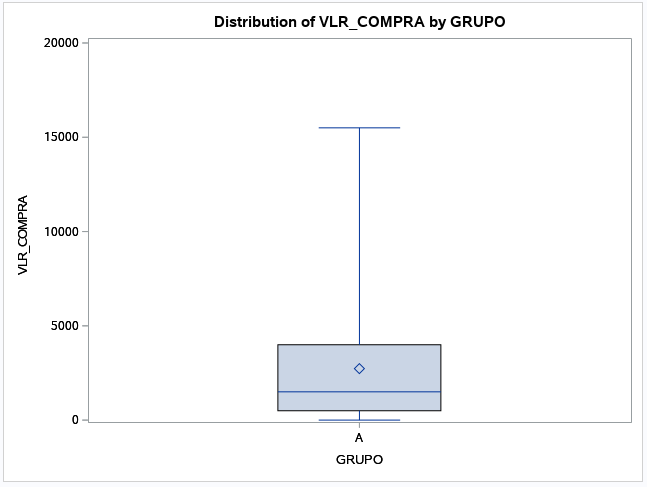
Você deve ter notado que os outliers foram incluídos sem serem destacados. Para criar um boxplot padrão, como o que mostramos no início do post, é preciso acrescentar o estilo do boxplot (boxstyle):

TITLE 'BOX PLOT';
PROC BOXPLOT DATA=EXEMPLO_4;
PLOT VLR_COMPRA*GRUPO/boxstyle=schematic;
RUN;

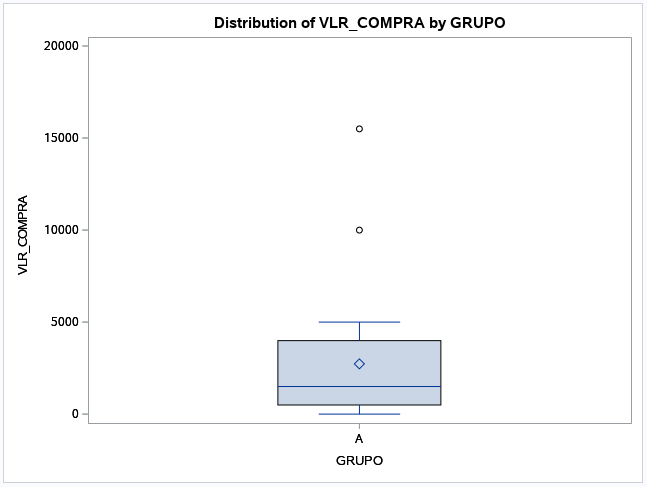
Agora sim, você já sabe o que é o intervalo interquartil, como ele se relaciona com o boxplot e como obter essas informações no SAS.

Espero ter ajudado. Se tiver alguma dúvida, crítica ou sugestão, comente no post ou mande uma mensagem no formulário que está em Sobre o Estatsite. Curte aí o post e compartilhe com seus colegas que têm interesse em aprender estatística, SAS, R, data science e afins.

Bons estudos!