Etiqueta: estatística

Visualizando a assertividade do seu experimento

Este post é um complemento ao Teorema de Bayes na prática: interpretando falso positivo e Probabilidade Condicional e o Teorema de Bayes. Apresento aqui uma demonstração visual de algumas medidas muito utilizadas na estatística.

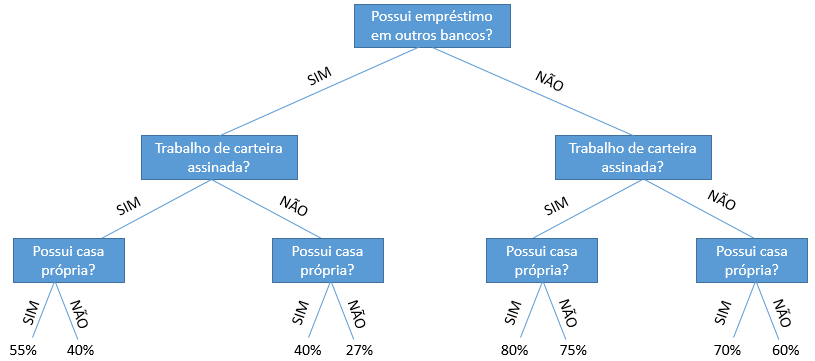
Dado um experimento em que queremos verificar se um exame é capaz de diagnosticar uma doença, temos os seguintes resultados possíveis:

 

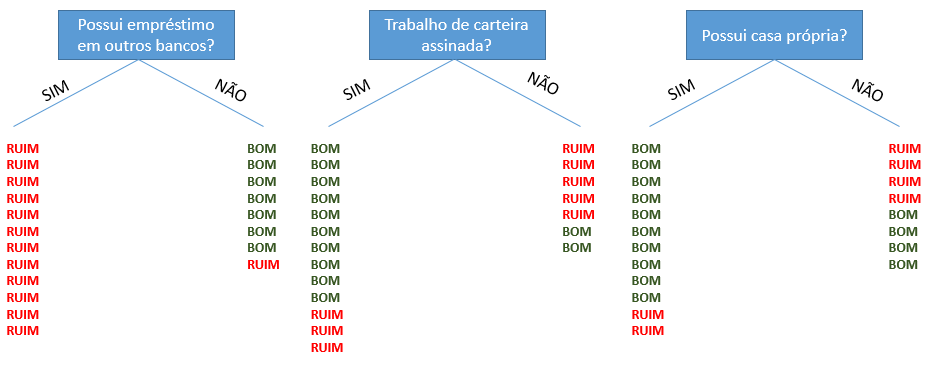
  • True Positive (TP) ~ Verdadeiro Positivo: O paciente foi diagnosticado como portador da doença e ele realmente é portador dela;
  • False Positive (FP) ~ Falso Positivo: O paciente foi diagnosticado como portador da doença, porém, ele não é portador dela;
  • False Negative (FN) ~ Falso Negativo: O paciente foi diagnosticado como não sendo portador da doença, porém, ele é portador dela;
  • True Negative (TN) ~ Verdadeiro Negativo: O paciente foi diagnosticado como não sendo portador da doença, e ele realmente não é portador dela.

A partir deste quadro, temos as seguintes medidas:

  • Sensibilidade: Probabilidade do exame ser positivo, dado que o paciente é portador da doença. Ou seja, capacidade do exame de acertar o diagnóstico de um paciente portador da doença;
  • Especificidade: Probabilidade do exame ser negativo, dado que o paciente não é portador da doença. Ou seja, capacidade do exame de acertar o diagnóstico de um paciente saudável;
  • Acurácia: Probabilidade do diagnóstico do exame estar correto.

Colocando em fórmulas matemáticas:

  • Sensibilidade = TP / (TP+FN)
  • Especificidade = TN / (FP+TN)
  • Acurácia = (TP+TN) / (TP+FN+FP+TN)

Veja que estamos falando de exames e doenças, mas essas medidas são utilizadas de diversas formas. Por exemplo, se você fizer uma regressão logística para prever inadimplência, você pode calcular a sensibilidade do seu modelo, qual a probabilidade de identificar um mau pagador, dado que o indivíduo é realmente mau pagador.

Probabilidade Condicional e o Teorema de Bayes

Seguindo a linha de obtenção da probabilidade quando temos mais de um evento, muitas vezes vamos querer saber a probabilidade de algo acontecer, dada alguma condição. Por exemplo, em uma escola podemos querer calcular a probabilidade do aluno ter nota vermelha, dado que é menino. Essa probabilidade pode ser diferente da probabilidade de se ter nota vermelha, dado que é uma menina. Para melhor visualização, considere a tabela abaixo com os alunos aprovados e reprovados nas primeiras provas de cada disciplina (tabela gerada com o randbetween() do excel):

Se escolhermos aleatoriamente um aluno, qual a probabilidade dele estar aprovado em matemática dado que é um menino?

Temos um total de 13 meninos, sendo que 6 estão aprovados. Logo, a probabilidade é 6/13.

A mesma pergunta, aplicado ao caso de que tenha sido escolhida uma menina resultaria em 5/14.

Ou seja, precisamos fazer pequenos ajustes no que consideramos nosso espaço amostral.

Utilizando as notações adequadas, temos que dado dois eventos A e B, a probabilidade condicional de A dado B, denotada por P(A|B) é:

P(A|B) = P(A∩B) / P(B)

Ou seja, no nosso exemplo, queremos P(aprovado | menino) e a resposta será a interseção dos dois eventos dividido pela probabilidade de ser menino.

A probabilidade de ser homem e estar aprovado em matemática é 6/27, temos 6 meninos aprovados em matemática de um total de 27 alunos.

Como temos 13 meninos em uma sala de 27 alunos, a probabilidade de ser menino é 13/27.

Logo, P(aprovado|menino) = 6/27 ÷ 13/27 = 6/13.

Isso é o que chamamos de probabilidade condicional.

Um teorema muito importante quando se fala de probabilidade condicional é o Teorema de Bayes. O que este teorema nos fornece é uma forma de relacionar as probabilidades condicionais ao seu inverso. Por exemplo, se você precisa saber a probabilidade de um evento A ocorrer dado que ocorreu um evento B, e você sabe a probabilidade de um evento B ocorrer dado que o evento A ocorreu, o teorema vai te levar a resposta. A fórmula principal do teorema é:

P(A|B) = P(A) x P(B|A) /  P(B)

BÔNUS: Agora, e se quisermos saber a probabilidade de sair coroa em um lançamento de moeda, dado que no lançamento anterior saiu cara?

Essa é uma pergunta que confunde muitas pessoas. Nem todos responderiam 1/2, que é a resposta correta.

Pense comigo, se você está lançando uma moeda, independente do que já aconteceu no passado, a chance de cair coroa é 50%. O fato de ter saído cara, ou coroa, em um primeiro lançamento não alterou nada na moeda que faça com que ela agora tenha um peso diferente e provavelmente vai sair cara (ou coroa). Se você quiser saber a probabilidade de ocorrer coroa nos dois lançamentos consecutivos, isso sim altera nosso resultado final, pois estamos avaliando os dois eventos simultaneamente. Parece besta para quem entende, mas muita gente comete este erro.

 

Probabilidade: E vs. OU

Exemplo 1: Vamos supor que você tenha um dado de seis faces e uma moeda honesta. Você decide realizar apostas e quem acertar o resultado de ambos ganhará um prêmio. Seu amigo aposta que sairá o número seis E cara. Qual a probabilidade dele estar certo? E qual seria a probabilidade se você facilitasse o jogo um pouco para ele, e deixasse que ele levasse um prêmio se acertasse um dos dois apenas?

Para responder a pergunta, você trabalhará com dois tipos de eventos.

O primeiro é uma intersecção (https://pt.wikipedia.org/wiki/Interse%C3%A7%C3%A3o), ou seja, quando ocorrem dois eventos simultaneamente, no caso o lançamento do dado resultar no número seis e o da moeda em cara.

O segundo caso, em teoria dos conjuntos, é uma união. Ou seja, se qualquer um dos eventos ocorrer, já satisfaço a condição.

Considerando o espaço amostral do experimento, temos:

Ω = {(c, 1), (c, 2), (c, 3), (c, 4), (c, 5), (c, 6), (k, 1), (k, 2), (k, 3), (k, 4), (k, 5), (k, 6)}

No caso da interseção, apenas o resultado (cara, 6) satisfaz. Ou seja, a probabilidade é 1/12.

No caso da união, há um conjunto de resultados que satisfazem, para ser mais preciso, 7 resultados satisfazem a condição para que o jogador ganhe:

{(c,1), (c, 2), (c, 3), (c, 4), (c, 5), (c, 6), (k, 6)}

Ou seja, no segundo jogo as chances do seu amigo ganhar aumentam muito, para 7/12.

Uma outra forma de fazer isso seria utilizando a multiplicação para o primeiro caso e a soma para o segundo.

Interseção: P(cara e 6) = P(cara) * P(6) = 1/2 * 1/6 = 1/12

União: P(cara ou 6) = P(cara) + P(6) = 1/2 + 1/6 = 7/12

Exemplo 2: Um dado foi lançado 3 vezes. Qual a probabilidade de sair 3 caras? E de sair ao menos uma cara?

P(3 caras) = 1/2 * 1/2 * 1/2 = 1/8

P(ao menos uma cara) = 1 – P (3 coroas) = 1 – (1/2 * 1/2 * 1/2) =

Essa de pelo menos uma cara pode confundir alguns, por isso resolvi colocar. Alguns poderiam fazer 1/2 + 1/2 + 1/2 = 3/2 = 150%. Mas como é possível uma probabilidade de 150%? Lembre-se de que probabilidade é um valor entre 0 e 1, escrevendo de outra forma, entre 0 e 100%. Isso não é possível porque aqui, se tivermos cara no primeiro caso, a nossa condição já está satisfeita para as demais. Para resolver este exercício, apresento aqui o conceito de complementar.

Sendo A um evento, o evento complementar de A são todos os eventos do espaço amostral que não estão contidos em A. Ou seja, se o evento é ocorrer cara, o complementar é ocorrer coroa. Se o que buscamos é que ocorra pelo menos uma cara, se considerarmos todas as opções que temos de eventos, o complementar do evento ‘ao menos uma cara’ é quando só ocorre coroa nos três lançamentos.

Visualmente: Wikipedia – Complementar

 

Primeiros Passos em Probabilidade

O QUE É PROBABILIDADE?

Produzi muito mais material de programação do que de estatística, por motivos óbvios: mais da metade do tempo gasto no trabalho é tratando as bases de dados. Isso é normal para qualquer um que trabalhe com modelagem estatística ou qualquer outro trabalho que utilize um volume grande de dados.

Por causa disso, acabei deixando um tema muito importante de fora: probabilidade!

Probabilidade é uma medida que varia de zero a um e que indica a chance de um evento ocorrer. Sendo que zero indica que não há chances do evento ocorrer e um indica que o evento ocorrerá com certeza.

Para se medir a probabilidade de um evento específico ocorrer devemos medir o número de vezes que este evento pode ocorrer pelo número total de eventos que podem ocorrer.

Exemplo 1: Qual a probabilidade de sair cara em um lançamento de uma moeda honesta?

Temos o evento cara, ou seja, um evento. E temos um total de dois eventos, pois o lançamento pode resultar em cara ou coroa. Logo, a resposta é:

1/2 = 0,5

Exemplo 2: Qual a probabilidade de tirarmos um número par no lançamento de um dado honesto?

O número de vezes que o evento ocorrer são 3, pois tiraremos um número par quando obtivermos o número 2, 4 ou 6 no lançamento.

O total de eventos que pode ocorrer é 6, pois podemos tirar 1, 2, 3, 4, 5 ou 6 no lançamento.

Sendo assim, a resposta é 3/6 = 1/2 = 0,5.

ESPAÇO AMOSTRAL

Note que você foi introduzido – sem notar – a um conceito novo que é amplamente utilizados na estatística: o espaço amostral.

Espaço amostral é o conjunto de todos eventos que podem ocorrer em um experimento. Por exemplo, o espaço amostral no lançamento de uma moeda é um conjunto de 2 elementos: cara e coroa. No caso do lançamento de um dado, o espaço amostral possui 6 elementos, os números 1, 2, 3, 4, 5 e 6.

O espaço amostral é usualmente denotado pela letra grega omega: Ω. Porém, em alguns casos você pode encontrar a letra U também, derivada do conceito de Universo.

Dado um espaço amostral Ω = {ω1, ω2, … , ωn}, onde ωi se refere ao evento i do experimento, P(ω) é a probabilidade do evento ω ocorrer.

Exemplo 3: Temos uma caixa com 3 bolas vermelhas, 5 bolas amarelas e 7 bolas verdes dentro. Qual o espaço amostral do experimento? Qual a probabilidade de eu tirar uma bola vermelha? E uma amarela? E uma verde? Qual cor tem mais chance de sair em uma retirada?

Ω = {vermelha, vermelha, vermelha, amarela, amarela, amarela, amarela, amarela, verde, verde, verde, verde, verde, verde, verde}

P(vermelho) = 3 / (3+5+7) = 3/15 = 1/5

P(amarela) = 5 / (3+5+7) = 5/15 = 1/3

P(verde) = 3 / (3+5+7) = 7/15

Note que a probabilidade de sair verde é maior que as demais. O que é bem intuitivo, afinal temos mais bolas verdes na caixa.

Simples não?

Lembre-se sempre da fórmula abaixo:

P(A) = N° de vezes que A ocorre / N° Total de Eventos que ocorrem

Árvore de Decisão

Uma das técnicas mais utilizadas para tomada de decisões é a árvore de decisões (em inglês decision trees). Sendo uma técnica capaz de lidar com a não linearidade, fácil de codificar, com poucas premissas e, talvez o mais importante, com resultado fácil de interpretar, a árvore de decisões é comumente adotada para concessões de crédito, diagnósticos médicos, análises de efeitos de drogas, análises de investimentos, etc.

A definição do wikipedia diz: “Uma árvore de decisão é uma representação de uma tabela de decisão sob a forma de uma árvore, porém podem haver outras aplicações. Tem a mesma utilidade da tabela de decisão. Trata-se de uma maneira alternativa de expressar as mesmas regras que são obtidas quando se constrói a tabela.”

Para ficar mais intuitivo, vamos pensar em um exemplo bem simples. O banco XYZ vai fornecer empréstimo a uma pessoa. Porém, sabemos que o banco XYZ não pode emprestar para qualquer um, não é todo mundo que vai pagar. Para decidir se vai ou não emprestar a uma pessoa, o banco XYZ monta um formulário com três perguntas:

  • Você possui empréstimo em outros bancos?
  • Você é casado?
  • Você possui casa própria?

Claro que o exemplo é um pouco banal, pois essa decisão depende de muitas variáveis, mas estamos querendo simplificar. Com base nas suas respostas, o banco deve decidir ou não dar um empréstimo. Ou seja, com base em um conjunto de respostas, o banco decide se você é um bom ou não pagador. Veja na árvore de decisões abaixo, que o banco XYZ, com base nas respostas dos clientes, sabe a probabilidade do cliente pagar ou não o empréstimo. E passa a fornecer crédito, para os clientes com probabilidade acima de 50%, que são os que ele considera bons pagadores:

Veja pelo diagrama, como é fácil identificar os clientes com os quais o banco irá fazer negócio. Isso nada mais é do que uma árvore de decisões.

Note que a árvore de decisões é uma ilustração de um algoritmo, um passo a passo que você realiza para tomar uma decisão, nesse caso a de emprestar ou não a um cliente.

E como você chega nessas probabilidades? Bom, lembre-se que já foi falado no blog como fazer modelos estatísticos nesse post. Para a árvore de decisões o raciocínio, normalmente, é o mesmo. Você possui alguns dados de clientes que já tomaram ou não empréstimos, suas características e se eles já pagaram ou não a sua dívida. Com base nisso, você saberá definir as melhores variáveis se baseando nas menor incerteza.

Por exemplo, suponha que o banco XYZ tenha 20 clientes que tomaram empréstimo no passado. Você está tentando decidir entre algumas variáveis para sua árvore de decisão. Para isso, você organiza o diagrama abaixo, sendo que bom é o cliente que pagou a dívida e ruim é o cliente que não pagou a dívida:

No diagrama, temos que dos 20 clientes da base do banco XYZ, dentre os que tomaram empréstimo em outros bancos, nenhum pagou a dívida. E dentre os que não tomaram, apenas um não pagou a dívida com o banco XYZ.

Com base na incerteza, podemos dizer que possuir empréstimo em outro banco é a melhor.

Veja que essa variável tem zero de incerteza, com base no histórico, todos os clientes que possuem empréstimo em outros bancos são maus pagadores.

E qual a pior variável?

Seguindo a mesma lógica, é a variável possui ou não casa própria. Veja que caso a pessoa não possua casa própria, a gente não consegue decidir se é mais provável que ela seja boa ou má pagadora. É equivalente a jogar uma moeda e decidir na sorte.

Leia também:

Árvore de Decisão no R
Árvore de Decisão com Probabilidade em R

Intervalo de Confiança: o que é e como estimar no SAS?

Intervalo de confiança nada mais é do que uma estimativa de um parâmetro de uma população.

Lembra de quando falamos de inferência estatística no post Estatística, Estatística Descritiva, Inferência Estatística?

Você tem uma amostra de uma população (um subgrupo) e a partir dela faz inferências a respeito da população. Os intervalos de confiança fazem isso para os parâmetros dessa população, eles inferem os valores reais e consideram um determinado grau de incerteza. Você vai conseguir, a partir de um parâmetro do seu subgrupo, estimar um parâmetro da população inteira.

Por exemplo, vamos supor que você tenha uma população de 100 milhões de pessoas e quer saber a altura média dessa população. Porém, para saber com certeza qual é a altura média da população inteira, você teria que medir todas as 100 milhões de pessoas, o que é praticamente impossível. Então, o que você faz?

Você pega uma amostra dessa população, de por exemplo 1.000 habitantes e calcula a altura delas. Você vai querer inferir a partir da altura média desses 1.000 habitantes, a altura média da sua população. Ou seja, você quer pegar essas 1.000 pessoas e com base nas informações delas, descobrir uma informação da população inteira de 100 milhões de pessoas.

Mas você sabe que a altura média das pessoas da amostra não vai ser exatamente a altura média da população, mas provavelmente algum valor próximo disso. Aí que entra o intervalo de confiança, ele é o intervalo no qual a altura da sua população estará contida, dado um grau de incerteza.

Se você chegar a conclusão que a altura da sua população está no intervalo de 1,70m a 1,75m com 95% de confiança, você quer dizer que se você coletar 100 amostras dessa população, 95 delas terão altura média no intervalo de 1,70m a 1,75m.

Simples, não?

E como calcular o intervalo de confiança no SAS?

Vejamos a amostra a seguir de uma população:

data amostra;
input altura;
cards;
1.70
1.68
1.80
1.72
1.55
1.66
1.78
1.90
2.00
1.57
2.70
1.78
1.59
1.54
1.53
1.70
;

proc print;
    var altura;
run;

Para calcular a média dessa população basta utilizar o proc summary com os parâmetros alpha, que será 1-nível de confiança, clm (confidence limits on the mean) e var seguido da variável em questão:

proc summary data=amostra print alpha=0.05 clm;
    var altura;
run;

Aqui temos um outro método que produz os mesmos resultados, porém com outros resultados que falaremos em futuros posts:

proc ttest data=amostra alpha=0.05; var altura; run;
Veja que o nosso exemplo o intervalo de confiança é relativamente amplo, ele é de 1,61 a 1,91. Isso parece bem intuitivo, afinal, temos poucas pessoas na amostra e um nível de confiança alto, seria como se nós estivéssemos querendo ter bastante certeza de que a média da população vai estar nesse intervalo. Parece razoável pensar que com poucas pessoas fica mais difícil ser preciso e como queremos ser bastante precisos (95%), só com um intervalo grande para “acertar” a média.

Média Móvel: Explicação, Comando SAS e Função LAG

A maioria das pessoas conhece e utiliza a média no dia a dia. O que alguns não conhecem é a média móvel. O que seria isso?

A média móvel nada mais é do que a média de um determinado número de observações recentes. Por exemplo, suponha que você seja dono de uma oficina e venda peças para automóveis. Suas vendas trimestrais estão representadas pela tabela abaixo:

Você é cauteloso com o seu orçamento, e, para decidir quanto gastar no ano seguinte, você quer verificar a tendência das vendas. Uma alternativa é utilizar a média móvel trimestral, que seria nada mais do que a média dos últimos três meses. Ou seja, você irá sempre pegar a média dos últimos três meses. Isso é útil para verificar se está havendo uma tendência de crescimento ou uma reversão, pois você captura movimentos recentes de vendas:

Simples, não?

Bônus – Média Móvel no SAS:

Para calcular a média móvel no SAS você precisará de algo que identifique os meses anteriores ao que você está analisando, isso pode ser obtido com a função lag().

Vamos supor que a tabela do exemplo acima foi criada no SAS com o nome BASE_VENDAS, contendo as variáveis: Ano e Vendas. Ao utilizar LAG(vendas), obteremos a variável vendas com uma defasagem. Ao utilizar LAG2(vendas), obteremos a variável vendas com duas defasagens:

data Variaveis_Defasadas;
    set Base_Vendas;
    Vendas_M1 = lag(vendas);
    Vendas_M2 = lag2(vendas);
run;

Esse é o resultado:


Agora ficou fácil descobrir como chegar a média móvel, certo?

data Media_Movel;
    set Variaveis_Defasadas;
    Media_3M = SUM(Vendas,Vendas_M1,Vendas_M2)/3;
    DROP Vendas_M1 Vendas_M2;
run;

Simples não?

Apenas para sanar quaisquer dúvidas:

SUM = Soma as variáveis, utilizando a vírgula para separá-las.

DROP = Exclui da tabela as variáveis (as colunas) que você não precisa mais.

Estatística, Estatística Descritiva, Inferência Estatística

Para quem já é do ramo parece algo trivial, mas para quem nunca viu, os nomes acima não são tão triviais. Sendo assim, acho que vale a pena explicar rapidamente aqui o que é cada um.

Estatística é o estudo de como coletar, organizar, analisar e interpretar dados. Pense em uma pesquisa eleitoral. Não é possível entrevistar todos os eleitores de um país. Sendo assim, técnicas estatísticas vão nos ensinar como coletar dados de forma a pegar uma amostra que represente a população ou saber quais as falhas a coleta pode ter. Além disso, é preciso saber o que retirar desses dados. Quem vota em qual político, qual a característica dos eleitores que votam no político X e quais as características de quem vota no político Y. Esse é apenas um exemplo dentre tantos que mostram como a estatística é utilizada.

Estatística descritiva é uma forma de sumarizar seus dados de forma quantitativa. É uma forma de resumir a informação que você possui. Pensemos agora em uma sala de aula. A professora tem a nota de todos seus alunos e quer saber como a classe está se saindo. Para isso, ela pode calcular a média, o mínimo, o máximo e o desvio padrão das notas dos alunos. Esses valores são estatísticas descritivas e estão passando para a professora uma ideia, um resumo, de como a sala dela está se saindo.

Por fim, temos a inferência estatística, que é o conjunto de técnicas para tirar conclusões dos seus dados. A inferência estatística é a parte em que a estatística tirará conclusões e deduzirá propriedades da sua população. Após você coletar uma amostra da sua população, você pode tirar algumas estatísticas descritivas dessa amostra mas e depois? Suponha que você queira saber quanto a família brasileira gasta. Você não consegue entrevistar todas as famílias do Brasil. O que você faz? Entrevista algumas e a partir disso, utilizando as técnicas corretas, deduz o quanto a família brasileira gasta. Note que estatística descritiva te dá apenas as informações da sua amostra coletada, sem deduzir nada, diferente da inferência, que é quando você irá traçar conclusões de toda a população com base na sua amostra.