Etiqueta: programacao em sas

Intervalo de Confiança: o que é e como estimar no SAS?

Intervalo de confiança nada mais é do que uma estimativa de um parâmetro de uma população.

Lembra de quando falamos de inferência estatística no post Estatística, Estatística Descritiva, Inferência Estatística?

Você tem uma amostra de uma população (um subgrupo) e a partir dela faz inferências a respeito da população. Os intervalos de confiança fazem isso para os parâmetros dessa população, eles inferem os valores reais e consideram um determinado grau de incerteza. Você vai conseguir, a partir de um parâmetro do seu subgrupo, estimar um parâmetro da população inteira.

Por exemplo, vamos supor que você tenha uma população de 100 milhões de pessoas e quer saber a altura média dessa população. Porém, para saber com certeza qual é a altura média da população inteira, você teria que medir todas as 100 milhões de pessoas, o que é praticamente impossível. Então, o que você faz?

Você pega uma amostra dessa população, de por exemplo 1.000 habitantes e calcula a altura delas. Você vai querer inferir a partir da altura média desses 1.000 habitantes, a altura média da sua população. Ou seja, você quer pegar essas 1.000 pessoas e com base nas informações delas, descobrir uma informação da população inteira de 100 milhões de pessoas.

Mas você sabe que a altura média das pessoas da amostra não vai ser exatamente a altura média da população, mas provavelmente algum valor próximo disso. Aí que entra o intervalo de confiança, ele é o intervalo no qual a altura da sua população estará contida, dado um grau de incerteza.

Se você chegar a conclusão que a altura da sua população está no intervalo de 1,70m a 1,75m com 95% de confiança, você quer dizer que se você coletar 100 amostras dessa população, 95 delas terão altura média no intervalo de 1,70m a 1,75m.

Simples, não?

E como calcular o intervalo de confiança no SAS?

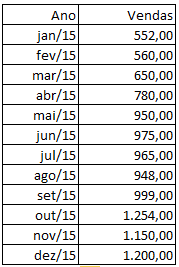
Vejamos a amostra a seguir de uma população:

data amostra;
input altura;
cards;
1.70
1.68
1.80
1.72
1.55
1.66
1.78
1.90
2.00
1.57
2.70
1.78
1.59
1.54
1.53
1.70
;

proc print;
    var altura;
run;

Para calcular a média dessa população basta utilizar o proc summary com os parâmetros alpha, que será 1-nível de confiança, clm (confidence limits on the mean) e var seguido da variável em questão:

proc summary data=amostra print alpha=0.05 clm;
    var altura;
run;

Aqui temos um outro método que produz os mesmos resultados, porém com outros resultados que falaremos em futuros posts:

proc ttest data=amostra alpha=0.05; var altura; run;
Veja que o nosso exemplo o intervalo de confiança é relativamente amplo, ele é de 1,61 a 1,91. Isso parece bem intuitivo, afinal, temos poucas pessoas na amostra e um nível de confiança alto, seria como se nós estivéssemos querendo ter bastante certeza de que a média da população vai estar nesse intervalo. Parece razoável pensar que com poucas pessoas fica mais difícil ser preciso e como queremos ser bastante precisos (95%), só com um intervalo grande para “acertar” a média.

Como calcular a diferença entre duas datas no SAS?

Novamente vou falar de datas no SAS. É sempre mais difícil trabalhar com datas em qualquer linguagem de programação. Por isso sempre que eu lembro de algo a respeito disso eu trato de escrever aqui porque acho que pode ajudar alguém. Dessa vez vamos aprender como descobrir a distância entre duas datas de algumas formas diferentes.

Voltando ao nosso exemplo dos alunos, nós já tínhamos suas notas e número de faltas, agora vamos acrescentar a data de nascimento deles:

data turma_1;
 input notas faltas dt_nasc ddmmyy10.; 
 format dt_nasc date9.; 
 datalines;
 3.6 13 20/02/1999
 3.6 15 15/04/1999
 5 9 02/10/1999
 6.4 8 01/05/1999
 6.6 7 10/03/1999
 6.6 8 12/11/1998
 6.8 8 14/08/1999
 7.5 5 23/02/1999
 8 4 30/07/1999
 8.7 3 08/03/1999
 9 1 24/02/1999
 9.5 1 15/11/1999
 ;
 proc print;
 run;

Veja como calcular a diferença entre as datas, primeiro de uma forma bem intuitiva apenas com a subtração entre a data de hoje e a do nascimento. Em seguida com as funções datdif e yrdif.

/*Acrescentando as colunas com diferença entre as datas*/
data Turma_1_v1;
    set Turma_1;
    dif_Dias=today()-dt_nasc;
    dif_Dias_2=datdif(dt_nasc,today(),'act/act');
    dif_Dias_3=datdif(dt_nasc,today(),'30/360');
    idade=yrdif(dt_nasc,TODAY());
run;

Como vocês podem ver, foram criados 3 campos utilizando fórmulas diferentes:

  1. Dif_Dias = Diferença entre o dia de hoje e a data de nascimento em dias;
  2. Dif_Dias2 = Diferença entre o dia de hoje e a data de nascimento em dias, utilizando o parâmetro ‘act/act’ para que o SAS entenda que a gente quer que o cálculo considere os dias reais entre as duas datas, considerando o número de dias que cada mês tem de acordo com o calendário;
  3. Dif_Dias3 = Diferença entre o dia de hoje e a data de nascimento em dias, utilizando como padrão que cada mês tem 30 dias e cada ano 360 dias. Isso pode ser útil para pessoas da área de finanças que precisam calcular retorno de alguns títulos;
  4. Idade = Diferença entre o dia de hoje e a data de nascimento em anos. Como não especificamos nada no terceiro parâmetro, o SAS nos traz a diferença considerando o calendário. O mesmo método utilizado em dif_dias poderia ter sido utilizado aqui.

Agora, ficou bem ruim essa idade com várias casas decimais. Eu recomendo trocar aquela linha por esse código com a função round:

idade=round(yrdif(dt_nasc,today()));

Função INTCK

Essa é mais uma função do SAS para lidar com datas, veja só como é intuitiva:

data Turma_1_v2;
set Turma_1;
    dif_meses=intck('month',dt_nasc,today());
    dif_anos=intck('year',dt_nasc,today());
    dif_dias=intck('day',dt_nasc,today());
    dif_semestres=intck('semiyear',dt_nasc,today());
    dif_trimestres=intck('qtr',dt_nasc,today());
run;

Nota: Se você estiver comparando duas datas do mesmo ano, dif_anos retornará zero. O mesmo vale para os demais. Caso você se confunda e coloque a data mais recente antes da data mais antiga, você receberá valores negativos (o que é intuitivo mas vale lembrar).

Gostou do post? Por favor, não vá embora sem deixar uma curtida ou um comentário. Parece algo bobo, mas é um feedback bastante importante para este trabalho. Se encontrou algum erro ou tem alguma sugestão, dúvida, elogio ou crítica, pode escrever nos comentários ou me enviar uma mensagem diretamente em Sobre o Estatsite. E visite também a conta do Twitter @EstatSite.

Forte abraço e bons estudos!

Média Móvel: Explicação, Comando SAS e Função LAG

A maioria das pessoas conhece e utiliza a média no dia a dia. O que alguns não conhecem é a média móvel. O que seria isso?

A média móvel nada mais é do que a média de um determinado número de observações recentes. Por exemplo, suponha que você seja dono de uma oficina e venda peças para automóveis. Suas vendas trimestrais estão representadas pela tabela abaixo:

Você é cauteloso com o seu orçamento, e, para decidir quanto gastar no ano seguinte, você quer verificar a tendência das vendas. Uma alternativa é utilizar a média móvel trimestral, que seria nada mais do que a média dos últimos três meses. Ou seja, você irá sempre pegar a média dos últimos três meses. Isso é útil para verificar se está havendo uma tendência de crescimento ou uma reversão, pois você captura movimentos recentes de vendas:

Simples, não?

Bônus – Média Móvel no SAS:

Para calcular a média móvel no SAS você precisará de algo que identifique os meses anteriores ao que você está analisando, isso pode ser obtido com a função lag().

Vamos supor que a tabela do exemplo acima foi criada no SAS com o nome BASE_VENDAS, contendo as variáveis: Ano e Vendas. Ao utilizar LAG(vendas), obteremos a variável vendas com uma defasagem. Ao utilizar LAG2(vendas), obteremos a variável vendas com duas defasagens:

data Variaveis_Defasadas;
    set Base_Vendas;
    Vendas_M1 = lag(vendas);
    Vendas_M2 = lag2(vendas);
run;

Esse é o resultado:


Agora ficou fácil descobrir como chegar a média móvel, certo?

data Media_Movel;
    set Variaveis_Defasadas;
    Media_3M = SUM(Vendas,Vendas_M1,Vendas_M2)/3;
    DROP Vendas_M1 Vendas_M2;
run;

Simples não?

Apenas para sanar quaisquer dúvidas:

SUM = Soma as variáveis, utilizando a vírgula para separá-las.

DROP = Exclui da tabela as variáveis (as colunas) que você não precisa mais.