Regressão Linear no Python

Como já expliquei em vários outros posts, Regressão Linear é uma técnica muito utilizada em modelagem – caso não se recorde, visite os posts Regressão Linear Simples – Parte 1, Regressão Linear Simples – Parte 2, Regressão Linear Simples – Parte 3 e Regressão Linear Múltipla. Em suma, um modelo linear será a soma ponderada de uma ou mais variáveis, chamadas de variáveis independentes ou explicativas, que irão predizer uma varável-alvo, também chamada de variável dependente ou resposta. Agora, vamos ver como você consegue rodar esse modelo no Python.

# Importa Bibliotecas
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression

# Cria datasets com 100 individuos
X_R1, y_R1 = make_regression(n_samples = 100, n_features=1,
n_informative=1, bias = 150.0,
noise = 30, random_state=0)

# Divide em treino e teste
X_train, X_test, y_train, y_test = train_test_split(X_R1, y_R1,
random_state = 1)

# Roda o modelo
linreg = LinearRegression().fit(X_train, y_train)

# Apresenta as informacoes desejadas
print('linear model coeff (w): {}'
.format(linreg.coef_))
print('linear model intercept (b): {:.3f}'
.format(linreg.intercept_))
print('R-squared score (training): {:.3f}'
.format(linreg.score(X_train, y_train)))
print('R-squared score (test): {:.3f}'
.format(linreg.score(X_test, y_test)))

No caso, a saída do código foi:

Isso significa que o nosso modelo tem um intercepto de 148,957 e um coeficiente de 44,31238628. Ou seja, para x = 0, nosso y será igual a 148,957, enquanto para x = 2, temos y aproximadamente 342,22.

Já o r-quadrado (ou coeficiente de determinação), conforme já dito em posts passados, representa o quanto da variabilidade de y é determinada por x. O valor do r-quadrado varia de 0 a 1.

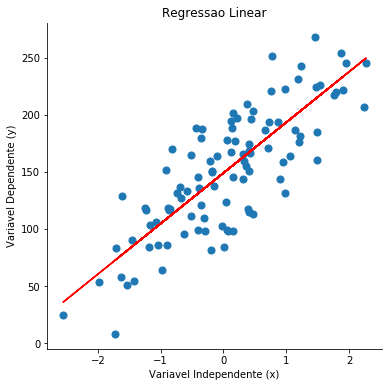
Para plotar o gráfico dessa regressão, incluindo a reta:

# importa biblioteca matplotlib
import matplotlib.pyplot as plt

# define tamanho do grafico
plt.figure(figsize=(6,6))

# traca grafico
plt.scatter(X_R1, y_R1, marker= 'o', s=50)
plt.plot(X_R1, linreg.coef_ * X_R1 + linreg.intercept_, 'r-')

# titulo principal
plt.title('Regressao Linear')

# rotulo de x
plt.xlabel('Variavel Independente (x)')

# rotulo de y
plt.ylabel('Variavel Dependente (y)')

# se quiser tirar a linha da direita e a de cima
ax = plt.gca()
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)

# se quiser definir a posicao dos 'ticks'
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')

plt.show()

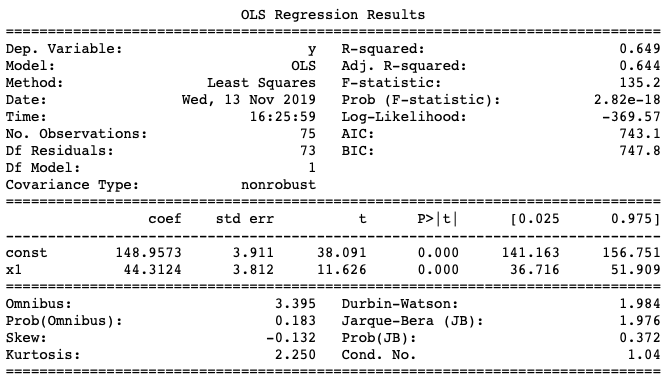
Note que a função do sklearn não disponibiliza as informações do p-valor, algo que é comum aos softwares estatísticos. Sendo assim, para os que desejam mostrar os p-valores, uma alternativa ao script acima é utilizar a biblioteca statsmodel:

import pandas as pd
import numpy as np
from sklearn import datasets, linear_model
from sklearn.linear_model import LinearRegression
import statsmodels.api as sm
from scipy import stats

X2 = sm.add_constant(X_train)
est = sm.OLS(y_train, X2)
est2 = est.fit()
print(est2.summary())

E se você gostou do post, não vá embora sem deixar uma curtida ou um comentário. Eu sei que não parece relevante, mas faz diferença para mim e custa pouco para você, vai… Se encontrou algum erro ou tem alguma sugestão, dúvida, elogio ou crítica, pode escrever nos comentários ou me enviar uma mensagem diretamente em Sobre o Estatsite. E visite também a conta do Twitter @EstatSite, costumo postar algumas coisas bem rapidinho por lá, geralmente são posts e códigos mais curtos ou compartilhamento de algo legal ou alguma reflexão.

Forte abraço e bons estudos!