ESTATSITE.COM.BR

O que é estatística?

Com a palavra, Peter Flom

Mais uma do Quora, dessa vez perguntaram O que é estatística?

Vou me aprofundar mais nisso no final de semana e introduzir um pouco de SAS no blog, mas gostaria de traduzir a resposta de Peter Flom – que mencionou outros estudiosos também – no forum do Quora, traduzida por mim:

Estatística é uma forma de separar sinal de ruído.

Estatística é um método de sumarizar dados.

Estatística é um método de fazer inferências a partir de una amostra da população.

Estatística é como biquinis. O que eles revelam é sugestivo mas o que eles ocultam é vital – Aaron Levenstein

Uma análise estatística, propriamente conduzida, é uma dissecação de incertezas, uma cirurgia de suposições. ~M.J. Moroney

Estatística pode ser definida como “um corpo de métodos para tomar decisões inteligentes quando se deparar com incerteza.~W.A. Wallis.

Domingo tem posts menos filosóficos e mais práticos!

Estatística, Estatística Descritiva, Inferência Estatística

Para quem já é do ramo parece algo trivial, mas para quem nunca viu, os nomes acima não são tão triviais. Sendo assim, acho que vale a pena explicar rapidamente aqui o que é cada um.

Estatística é o estudo de como coletar, organizar, analisar e interpretar dados. Pense em uma pesquisa eleitoral. Não é possível entrevistar todos os eleitores de um país. Sendo assim, técnicas estatísticas vão nos ensinar como coletar dados de forma a pegar uma amostra que represente a população ou saber quais as falhas a coleta pode ter. Além disso, é preciso saber o que retirar desses dados. Quem vota em qual político, qual a característica dos eleitores que votam no político X e quais as características de quem vota no político Y. Esse é apenas um exemplo dentre tantos que mostram como a estatística é utilizada.

Estatística descritiva é uma forma de sumarizar seus dados de forma quantitativa. É uma forma de resumir a informação que você possui. Pensemos agora em uma sala de aula. A professora tem a nota de todos seus alunos e quer saber como a classe está se saindo. Para isso, ela pode calcular a média, o mínimo, o máximo e o desvio padrão das notas dos alunos. Esses valores são estatísticas descritivas e estão passando para a professora uma ideia, um resumo, de como a sala dela está se saindo.

Por fim, temos a inferência estatística, que é o conjunto de técnicas para tirar conclusões dos seus dados. A inferência estatística é a parte em que a estatística tirará conclusões e deduzirá propriedades da sua população. Após você coletar uma amostra da sua população, você pode tirar algumas estatísticas descritivas dessa amostra mas e depois? Suponha que você queira saber quanto a família brasileira gasta. Você não consegue entrevistar todas as famílias do Brasil. O que você faz? Entrevista algumas e a partir disso, utilizando as técnicas corretas, deduz o quanto a família brasileira gasta. Note que estatística descritiva te dá apenas as informações da sua amostra coletada, sem deduzir nada, diferente da inferência, que é quando você irá traçar conclusões de toda a população com base na sua amostra.

O câmbio e a cointegração

Em um excelente post em seu blog, Marcelo Curado fala da aposta de muitos economistas em uma recuperação da economia brasileira graças a desvalorização do real. Em um texto curto e bem bacana ele acaba com esse pensamento.

O que é mais intuitivo é que o câmbio quando desvaloriza eleva nossa exportações (porque os produtos ficam mais baratos para os gringos), ou seja, mais money entrado para a gente, e também aumenta a produção local, já que a gente não vai importar porque vai estar tudo caro.

Ele dá diversas evidências de que esse pensamento que parece tão óbvio não é tão verdade assim. Vale a leitura, não é complexo e o professor, como de costume, faz uma análise interessante.

Como estou aqui para falar de econometria, o que me chamou a atenção foi o teste de cointegração feito no post. O que seria isso?

Cointegração serve para indicar se duas séries temporais possuem uma relação de longo prazo. Colocada da forma mais simples possível, cointegração indica se as duas variáveis estão se movendo numa mesma tendência.

Uma história bem comum que você vai ouvir quando ler explicações sobre cointegração é a do bêbado e seu cachorro. Pense que os dois andam de forma aleatória, mas há aí uma relação, porque eles sempre estarão perto. Apesar de cada um andar de forma aleatória, os dois tem uma conexão, o cachorro vai seguir o dono, ou o contrário. Eles tem uma certa conexão e a distância de um ao outro é previsível de certa forma. O bêbado e o cachorro formam um par cointegrado. Embora tenham passeios aleatórios, conseguimos prever a distância entre os dois e aí nasce a cointegração.

Qual a importância disso?

Primeiro porque podemos estudar essas relações de pares. Pensando para o lado de finanças, ficaria muito mais fácil você bolar estratégias de negociação de pares de ações. Você sabe como as duas se comportam entre si, fazendo com que você possa por exemplo comprar uma e vender outra a determinados preços de forma que você ganhe uma grana, já que você sabe a distância entre os preços das duas.

E o principal é que muitas de nossas técnicas falham quando lidamos com dados não estacionários, por isso esse teste é melhor. Estamos evitando relações espúrias.

E o que é estacionário?

Um processo estacionário é aquele que a média, variância e autocorrelação não muda ao longo do tempo. Mas falamos mais sobre isso em um post futuro!✌️

Viés de Seleção: Seus resultados podem estar te enganando

Imagine que você queira saber se pessoas que vão ao médico vivem melhor do que pessoas que não vão, ou vão pouco, ao médico. Aí você monta um experimento, pega 100 pessoas que vão ao médico semanalmente e outras 100 que quase não vão. Ao final de um período você analisa os dois grupos e olhe só, quem menos foi ao médico está mais saudável. É suficiente para você concluir que ir ao médico faz mal à saúde?

Você pode levantar diversas hipóteses aí. Talvez ir ao médico seja ruim porque você pega doenças de outros pacientes, ou então os médicos não tratam direito os pacientes, ou quem vai ao médico toma muitos remédios e os efeitos colaterais são ruins.

É bem possíve que você tenha sido mais uma vítima do viés de seleção.

O viés de seleção ocorre quando o grupo estudado não foi escolhido de forma aleatória. Mesmo que não intencional, afinal, nesse caso você não escolheu os seus pacientes, mas nem por isso a escolha foi aleatória.

Pense no exemplo mencionado. Pessoas que vão ao médico constantemente, na maioria das vezes, vão porque possuem uma saúde mais debilitada que pessoas que não vão tanto ao médico. Sendo assim, é muito provável que elas possuam uma saúde pior mesmo indo ao médico.

Outro exemplo poderia ser algumas pesquisas antigamente que eram feitas por telefone. Imagine que uma empresa ligue para diversas pessoas para fazer uma determinada pesquisa. Mesmo que ela ligue para pessoas de diversas cidades, essa amostra possivelmente está viesada, já que muitas pessoas não possuíam telefone em casa no Brasil.

Sempre que ler um estudo, ou fizer seu próprio estudo, pense bem em como sua amostra foi selecionada, isso vai fazer toda a diferença!

Para os que possuem inglês de nível avançado ou fluente, recomendo a leitura do livro Mostly Harmless Econometrics de Joshua Angrist, os capítulos 1 e 2 dão uma boa ideia desse tipo de problema.

Intervalo de Confiança

Um post bem rápido aqui só para corrigir uma interpretação equivocada de muitas pessoas.

Quando você ouvir algo do tipo “o candidato X tem 45% dos votos, com uma margem de erro de 5%”, assumindo que isso seja com 95% de confiança, não quer dizer que tem 95% de chance do candidato ter de 40% a 50% dos votos. Na verdade, quer dizer que há 95% de probabilidade que seu intervalo contenha o valor correto.

A diferença é sutil, eu acho até um pouco de exagero implicar com isso, mas vale ter esse cuidado já que tantos livros implicam com essa diferença.

Análise dos Resíduos de uma Regressão Linear

Conforme já foi falado neste blog, os resíduos de uma regressão linear são as diferenças entre os pontos observados e a curva que estimamos. Ou seja, você tem lá valores reais que você observou do fenômeno que está analisando e tem a equação da reta que você estimou através de um método qualquer. A diferença entre esses dois valores é o seu resíduo.

Por exemplo, suponha que você queira saber quanto o imposto sobre bebidas alcoólicas e o limite de velocidade de uma via afetam o número de acidentes. Utilizando um método qualquer, você obtém a equação abaixo.

Onde yi é o número de acidentes na via i, β1 é o imposto sobre bebidas alcoólicas e β2 é o limite de velocidade nesta via.

Se tivermos a avenida XPTO em uma cidade em que o imposto sobre as bebidas é de 20% e o limite de velocidade desta via for 60 km/h, nossa equação nos diz que o número de acidentes da via X deve ser de 100 – 14*0,2 + 0,5* 60 = 127,2.

Observamos que na avenida X, o número de acidentes no mês foi 130. Ou seja, nosso resíduo aqui é de 2,8.

Por enquanto tudo tranquilo, certo?

Agora que já entendemos claramente o que é o resíduo, precisamos saber como analisá-lo. Lembre-se que o resíduo deve ter esperança zero. Colocado de maneira prática, o que você precisa, é plotar os valores o seu resíduo com sua variável resposta e obter este gráfico:

Veja que nossos resíduos estão transitando ao redor de zero e que independente do número de acidentes ser alto ou baixo, os resíduos tem esperança zero. É isso que buscamos para ter um modelo mais preciso possível.

Abaixo mais alguns exemplos de resíduos plotados com as variáveis respostas, note que o gráfico maior a esquerda possui resíduos bem comportados, enquanto os da direita não parecem ter esperança zero e possuem uma tendência, eles variam de acordo com a grandeza da variável resposta:

Problemas com R? Que tal começar em Primeiros passos no R Studio!

Curtose

A curtose é uma medida que, conforme falado no post anterior, aparece na sua estatística descritiva do excel. Porém, a maioria das pessoas não a conhece. Tranquilão, aqui vai um resumo deboas para você:

O que a curtose nos fornece é simplesmente o quão achatado é o “pico” da nossa distribuição de frequência.

Veja as três distribuições abaixo:

Elas mostram como nossos dados estão distribuídos. No primeiro caso, nossa curva parece uma normal. No segundo gráfico, nossos dados estão mais concentrados no ponto central. Já no último gráfico, nossos dados estão menos concentrados.

Beleza, agora já entendemos o motivo de estudarmos a curtose e o que é exatamente esse “achatamento” do pico. Queremos entender como nossos dados estão distribuídos, simples. E como utilizamos o número que o excel nos fornece?

Só para constar, o que o excel nos dá, colocando de uma forma mais formal, é o que chamamos de excesso de curtose.

Tá, blá blá blá, whatever… o que isso significa?

Significa que se o excel “cuspir” uma curtose próxima de 3, sua distribuição parecerá uma normal, se for menor que 3 então teremos um pico um pouco mais fino e se maior que 3 um pico mais achatado, parecido com aquele terceiro gráfico acima.

E aqueles nomes em cima dos gráficos? É só uma forma mais legal de chamar a nossa distribuição. Só para reforçar, mais uma vez:

Se a curtose for menor que 3, distribuição é leptocúrtica

Se a curtose for próxima de 3 a distribuição é mesocúrtica

Se a curtose for maior que 3 distribuição é platicúrtica.

Estatística Descritiva

Estatística descritiva, como o próprio nome já diz, é uma disciplina (ramo, técnica, etc.), que utilizamos para descrever dados de forma quantitativa.

Quando você está no excel e vai em análise de dados, você pode selecionar estatística descritiva e marcar a caixinha “resumo estatístico” para obter diversas informações a respeito dos seus dados. Farei aqui um breve resumo do que é cada uma das principais estatísticas fornecida pelo Excel.

Antes, vamos lembrar algumas definições básicas.

A média, mediana e moda, são chamadas de medidas de tendência central. Como o próprio nome diz, elas fazem referência ao centro da nossa distribuição. Ou seja, onde nossos dados estão centrados, qual o “meio” da nossa distribuição.

Em contrapartida, mediana, variância e desvio padrão são medidas de dispersão. Servem para mostrar o quanto nossos dados estão dispersos.

Por exemplo, suponha que a gente tenha duas cidades, A e B, com 10 moradores cada e com os seguintes salários:

Cidade A: $200, $200, $200, $200, $200, $200, $200, $200, $200, $200;

Cidade B: $10, $10, $10, $10, $10, $100, $100, $100, $100, $1550.

A média da cidade A e da cidade B é $200, mas o desvio padrão da cidade A é 0 e da cidade B é 451,99. Ou seja, os dados da cidade B estão bem mais dispersos. Podemos ver que os salários na cidade A são bem distribuídos, enquanto na cidade B há uma diferença significante entre os salários. Por esse motivo, é importante conhecermos tanto as medidas de tendência central, quanto as medidas de dispersão.

Vejamos agora as principais estatísticas fornecidas pelo Excel e o que significa cada uma:

Média: Média aritmética da sua amostra, provavelmente a estatística mais conhecida e utilizada por todos, imagino que não precise de muita explicação. Nada mais é do que a soma das suas observações dividido pelo número de observações.
Erro padrão: Estima a variabilidade de suas amostras, sua fórmula é o desvio padrão dividido pelo tamanho da amostra.
Mediana: Valor que está no centro da sua amostra, metade dos valores está acima deste número e metade abaixo. Na cidade A a mediana é 200 e na cidade B é 55, pois (10+100)/2 = 55.
Moda: Valor que aparece mais vezes nos seus dados. Na cidade A a moda é 200 e na cidade B é 10.
Desvio padrão: Mede o quanto seus dados variam com relação a média.
Variância: Essa medida vai te dar a dispersão dos seus dados com relação a média, mas em uma dimensão que será o quadrado da dimensão dos seus dados.
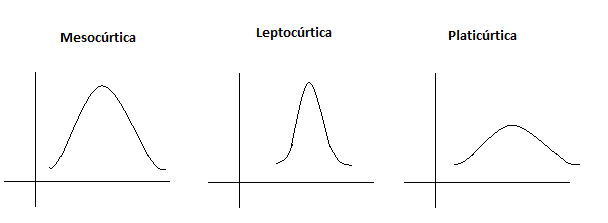
Curtose: Também é uma medida para indicar a dispersão dos seus dados, mas nesse caso, a estatística nos dará o quão achatado é o gráfico da função de probabilidade dos nossos dados. Falaremos mais dessa medida em um post futuro, por enquanto, ficamos com a definição mais básica de que uma Curtose próxima de zero indica uma distribuição normal.
Assimetria: Nos dá a simetria da distribuição dos nossos dados. Como assim? Bem, se você desenhar a curva de distribuição dos seus dados, você pode ter algo parecido com uma normal, uma curva um pouco mais concentrada a direita e caindo quando vai para a esquerda, ou o contrário. É isso que a essa medida do excel nos ajuda a entender. Uma distribuição simétrica, que tem o formato de um sino, terá assimetria igual a 0. No entanto, se a distribuição possuir uma maior concentração de dados a esquerda, o valor dessa estatística será negativo.

A Matemática como um hobby

Esse blog vai sempre focar em estatística e econometria, mas a matemática tem sua conexão com essas duas disciplinas, sendo assim, eu, graduado em Licenciatura em Matemática, obviamente vou falar dela.

Eu sempre notei que as pessoas não conseguem entender o amor aos números. Sempre sobram comentários em tons de brincadeira, mas muitas vezes sobram comentários sérios. Eu não ligo para as brincadeiras porque senso de humor não falta em mim e eu sou o que mais encho todo mundo com brincadeiras. Mas comecei a achar interessante o quanto as pessoas não conseguem entender o prazer em estudar e ler sobre matemática. Que o “vício” por números é igual ao vício por futebol, música, livros em geral, etc. Que a matemática pode ser um hobby e não tem nada de errado nisso. Não sou menos feliz porque meu hobby são os números. Na verdade, acho que sou até mais feliz porque sou pago para trabalhar com isso. Imagine você corinthiano fanático sendo pago para assistir seu time? Você cinéfilo sendo pago para ir ao cinema em todo lançamento? É o sonho!

Correndo o risco de ser taxado de nerd sem vida virgem esquisito, para mim é isso, eu seria o corinthiano sendo pago para ver o coringão em campo ou o cinéfilo sendo pago para ir ver os lançamentos da Marvel ou o novo Star Wars. Esse sentimento é bom pra c…!!!

Pensando nisso, lancei uma pergunta no Quora que dizia: “Eu gosto muito de Matemática e as pessoas não entendem isso. Como eu posso explicar que isso pode ser um hobby?”

As opiniões e experiências compartilhadas não decepcionaram:

I really enjoy Math…

Alguns dos meus trechos preferidos:

“As pessoas enxergavam a matemática como se fosse algo a 180° de arte, mas não era. A matemática também abraça os ideais de harmonia, balanço, estrutura e elegância na expressão. Há forma, significado, filosofia e surpresa lá também. Eu disse a eles que existe tanta beleza em matemática quanto em qualquer lugar que eu já tenha perseguido…”

“As pessoas têm todos os tipos de hobbies, alguns, honestamente, bizarros. Você consegue imaginar ser tão fascinado pelos rótulos das comidas enlatadas e gastar todo seu tempo livre coletando, preservando e catalogando rótulos de comidas enlatadas? Eu aposto que isso é o hobbie de alguém… Mas se as pessoas não conseguem entender por que e como a matemática é um objeto de fascinação seu, eu diria que essas pessoas não pegaram a natureza real da matemática. A matemática, assim como lógica, é bela…

nós vivemos em uma sociedade onde colecionar bonecas da barbie é um hobbie aceitável mas matemática é um hobbie que leva à chacota?”

“O ato de desacelerar e dedicar um esforço mental real a uma tarefa é algo que deixa a maioria das pessoas… desconfortável, para dizer o mínimo.

Eu não quero dizer algo tão elitista quanto sugerir que a matemática está além da maioria das pessoas, porque não está. Eu só quero dizer que a maioria das pessoas não entende porque alguém colocaria tanto esforço em qualquer coisa. Nós nos tornamos viciados em emoções baratas e no encanto de recompensas imediatas.”

Erros vs. Resíduos

É comum cometermos o equívoco de chamar erros de resíduos e vice-versa. A definição é próxima mesmo, então não se preocupe se você já cometeu esse erro. Enfim, qual a diferença entre o que chamamos de erros e dos chamados resíduos?

O erro é a diferença entre o valor real, que não observamos, e o valor estimado. Já o resíduo é a diferença entre o valor estimado e o valor observado.

Confuso? Eu sempre achei, então vamos tentar de novo.

Quando realizamos nossa regressão, estamos tentando estimar uma reta que melhor se aproxima do conjunto de pontos que temos observado, mas nós nunca sabemos qual é a reta real que explicaria esse conjunto de pontos. O que nós conseguimos é uma estimativa dessa reta.

Vamos supor que tenhamos uma população onde o peso médio é 70kg e temos um indivíduo retirado aleatoriamente dessa população que pesa 65kg. Então o erro desse indivíduo é -5kg.

Em contrapartida, quando falamos de resíduos, estamos buscando uma estimativa do erro não observado. Nesse caso, estamos falando, por exemplo, de retirar uma amostra aleatória de uma população e tiramos a média amostral. A diferença entre a média amostral e algum indivíduo retirado dela, isso sim é o resíduo!

Facilitou?