Arquivo de Ciência de Dados - Página 8 de 9

Viés de Variável Omitida: Um exemplo prático

Já mencionei o viés de variável omitida no post Quanto mais polícia, mais crimes? e Paradoxo de Simpson, vamos ver mais um exemplo prático.

Vamos supor que você queira analisar o impacto do número de professores em uma escola com as notas dos alunos. Ou seja, você gostaria de estimar os beta 1 da seguinte equação:

média das notas = β0 + β1*n° de professores + u

É de se esperar que β1 seja maior que 0, pois a expectativa é que um número maior de professores seja benéfico para os alunos por diversos motivos.

Entretanto, pensemos nas variáveis não utilizadas no modelo e que “alocamos” em u. Dentre essas variáveis, temos, por exemplo, o investimento do governo nessas escolas. Afinal, um governo que investe mais, tenderá a contratar mais professores para suprir todas as necessidades da escola. Ou seja, a correlação entre número de professores e investimento do governo é positiva, quanto maior o investimento feito, maior o número de professores. Note que a esperança do u dado o parâmetro n° de professores não é zero. Afinal, como já dissemos, quanto maior o investimento de um governo, maior o número de professores, sendo assim, violamos uma premissa da nossa regressão OLS (ordinal least squares).

Ε (u | n° de professores) ≠ 0

É provável que se calcularmos um coeficiente de valor 10, este valor seja na verdade um valor menor qualquer como 7 ou 5. Isso ocorre porque o parâmetro n° de professores está absorvendo parte do impacto que o investimento do governo causa. O resultado é que nosso coeficiente está com viés, superestimando o impacto da variável.

Este é o problema de se omitir uma variável relevante.

Baseado em: Omitted Variable Bias – Ben Lambert

Paradoxo de Simpson

O paradoxo de Simpson é um caso em que quando examinamos grupos diferentes observamos uma tendência que se altera quando combinamos estes grupos.

Um exemplo clássico é o caso de admissão de mulheres na Universidade de Berkeley. Acreditava-se que as mulheres estavam sendo discriminadas na admissão, pois o percentual de mulheres admitidas era muito menor que o percentual de homens, conforme podemos observar na tabela abaixo:

Entretanto, quando a análise era feita por departamento, isto não ocorria. A tabela abaixo apresenta os dados dos seis maiores departamentos da universidade, veja que dos 6, em apenas 2 o percentual de homens admitidos era menor:

A interpretação equivocada ocorreu porque havia maior concentração de mulheres aplicando em departamentos com menor taxa de admissão.

Isso ocorre simplesmente porque existe uma variável que se correlaciona tanto com a variável dependente quanto com a independente. Em outras palavras, é mais um caso de viés de variável omitida.

Obs.: Variável omitida é uma variável não considerada/avaliada por quem está fazendo a pesquisa. Esta variável é incorporada ao erro, porém, se uma variável importante é deixada de fora do modelo, o modelo poderá ter seus estimadores com viés e inconsistentes.

Empréstimos inteligentes para pessoas sem histórico de crédito

Muitas pessoas não sabem o que faz uma pessoa que trabalha com modelagem estatística. E olha que isso pode estar presente no job description de muitos cargos: analista de risco de crédito, inteligência de cobrança, inteligência de mercado, cientista de dados, CRM, big data, pesquisa de mercado, só para citar alguns.

Então vai aí um exemplo prático, e nobre, do uso de modelagem estatística e mineração de dados:

Explicando overfitting com uma anedota

Uma anedota bem interessante foi sugerida por uma escritora do Quora chamada Divya Sharma:

O pequeno Bobby ama cookies. Sua mãe faz cookies de gotas de chocolate todos os domingos. Porém, o mundo não é o ideal e os cookies não possuem o mesmo sabor todo domingo. Alguns domingos eles estão mais saborosos, outros domingos eles não estão tão bons. Sendo o pequeno menino curioso que é, Bobby decide descobrir quando os cookies ficam mais saborosos e quando não ficam.

A primeira observação que ele faz é que o número de gotas de chocolate varia de cookie pra cookie e essa é praticamente a única coisa observável que varia entre os cookies.

Agora, Bobby começa a tomar notas todos os domingos.

Depois de sete domingos, as suas notas parecem com algo assim:

Domingo 1 – No. de Gotas de Chocolate: 7; Sabor: Ótimo
Domingo 2 – No. de Gotas de Chocolate: 4; Sabor: Bom
Domingo 3 – No. de Gotas de Chocolate: 2; Sabor: Ruim
Domingo 4 – No. de Gotas de Chocolate: 5; Sabor: Horrível
Domingo 5 – No. de Gotas de Chocolate: 3; Sabor: Mais ou menos
Domingo 6 – No. de Gotas de Chocolate: 6; Sabor: Horrível

Isso parece bem direto. Quanto maior o número de gotas de chocolates, mais saboroso o cookie, com exceção das anotações de domingo 4 e domingo 6, que contradizem esta hipótese. O que o pequeno Bobby não sabe é que sua mãe esqueceu de colocar açúcar nos cookies de domingo 4 e domingo 6.

Como Bobby é uma pequena criança inocente, ele não sabe que o mundo está longe do ideal e que coisas como aleatoriedade e ruído são parte integral dele. Ele também não sabe que há fatores que não são diretamente observáveis. Porém, eles afetam o resultado de nossos experimentos. Então, ele conclui que o cookies ficam mais gostosos na medida que o número de gotas de chocolate aumentam quando há menos que 5 gotas de chocolate e mais que 6, mas caem drasticamente quando o número de gotas de chocolate é 5 ou 6.

Ele levantou uma hipótese muito complexa, e, não vamos nos esquecer, incorreta, para explicar como o sabor dos cookies variam porque ele tentou explicar e justificar as anotações de cada um dos domingos. Isso é chamado sobreajuste. Tentar explicar/justificar o máximo de observações possíveis com uma hipótese extremamente complexa – e possivelmente incorreta.

Se ele tivesse escolhido tratar o domingo 4 e o domingo 6 como ruídos, a hipótese dele teria sido mais simples e relativamente mais correta.

Traduzido de https://www.quora.com/What-is-an-intuitive-explanation-of-overfitting/answer/Divya-Sharma-2?srid=GcIk

Overfitting e Cross Validation

Um termo bem comum de se encontrar quando o assunto é modelagem é overfitting. É até bonito de se dizer. Overfitting ocorre quando o seu modelo se ajusta perfeitamente aos seus dados, ou seja, o modelo serve só para os dados da base que foi utilizada para a sua construção. O que ocorre é que nesse caso o modelo passa em diversos testes de precisão com o conjunto de dados utilizados, porém, não serve para predição. Em outras palavras, como alguns cientistas de dados costumam dizer, o seu modelo aprender os dados da base treino ao invés de aprender o todo e ser capaz de fazer previsões. A grosso modo, isso ocorre quando você possui uma alta complexidade e muitos parâmetros se comparado com a base de desenvolvimento. Nesse caso, o modelo serve somente para os dados utilizados no desenvolvimento e suas previsões serão fracas. Continuar a ler “Overfitting e Cross Validation”

Árvore de Decisão no R

Árvore de decisão é um modelo simples e extremamente útil para fazer predições. É fácil de explicar para as pessoas mais alheias ao mundo de ciência de dados e machine learning. Além disso, é simples de identificar o poder preditivo das variáveis, requer pouco pré-processamento, etc. Hoje, vou apresentar o código em R para uma árvore de decisão. Continuar a ler “Árvore de Decisão no R”

Árvore de Decisão

Uma das técnicas mais utilizadas para tomada de decisões é a árvore de decisões (em inglês decision trees). Sendo uma técnica capaz de lidar com a não linearidade, fácil de codificar, com poucas premissas e, talvez o mais importante, com resultado fácil de interpretar, a árvore de decisões é comumente adotada para concessões de crédito, diagnósticos médicos, análises de efeitos de drogas, análises de investimentos, etc.

A definição do wikipedia diz: “Uma árvore de decisão é uma representação de uma tabela de decisão sob a forma de uma árvore, porém podem haver outras aplicações. Tem a mesma utilidade da tabela de decisão. Trata-se de uma maneira alternativa de expressar as mesmas regras que são obtidas quando se constrói a tabela.”

Para ficar mais intuitivo, vamos pensar em um exemplo bem simples. O banco XYZ vai fornecer empréstimo a uma pessoa. Porém, sabemos que o banco XYZ não pode emprestar para qualquer um, não é todo mundo que vai pagar. Para decidir se vai ou não emprestar a uma pessoa, o banco XYZ monta um formulário com três perguntas:

Você possui empréstimo em outros bancos?
Você é casado?
Você possui casa própria?

Claro que o exemplo é um pouco banal, pois essa decisão depende de muitas variáveis, mas estamos querendo simplificar. Com base nas suas respostas, o banco deve decidir ou não dar um empréstimo. Ou seja, com base em um conjunto de respostas, o banco decide se você é um bom ou não pagador. Veja na árvore de decisões abaixo, que o banco XYZ, com base nas respostas dos clientes, sabe a probabilidade do cliente pagar ou não o empréstimo. E passa a fornecer crédito, para os clientes com probabilidade acima de 50%, que são os que ele considera bons pagadores:

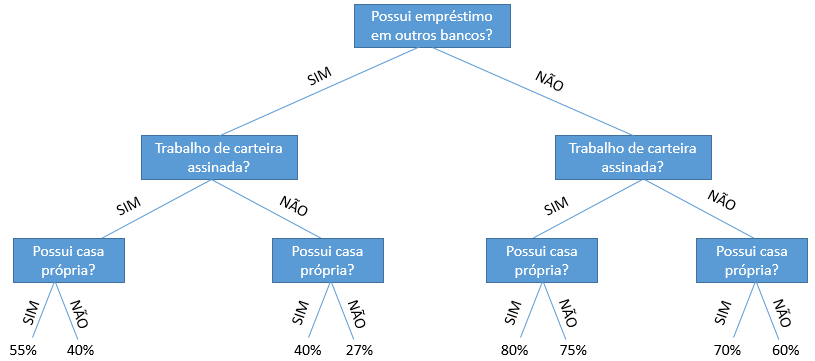
Veja pelo diagrama, como é fácil identificar os clientes com os quais o banco irá fazer negócio. Isso nada mais é do que uma árvore de decisões.

Note que a árvore de decisões é uma ilustração de um algoritmo, um passo a passo que você realiza para tomar uma decisão, nesse caso a de emprestar ou não a um cliente.

E como você chega nessas probabilidades? Bom, lembre-se que já foi falado no blog como fazer modelos estatísticos nesse post. Para a árvore de decisões o raciocínio, normalmente, é o mesmo. Você possui alguns dados de clientes que já tomaram ou não empréstimos, suas características e se eles já pagaram ou não a sua dívida. Com base nisso, você saberá definir as melhores variáveis se baseando nas menor incerteza.

Por exemplo, suponha que o banco XYZ tenha 20 clientes que tomaram empréstimo no passado. Você está tentando decidir entre algumas variáveis para sua árvore de decisão. Para isso, você organiza o diagrama abaixo, sendo que bom é o cliente que pagou a dívida e ruim é o cliente que não pagou a dívida:

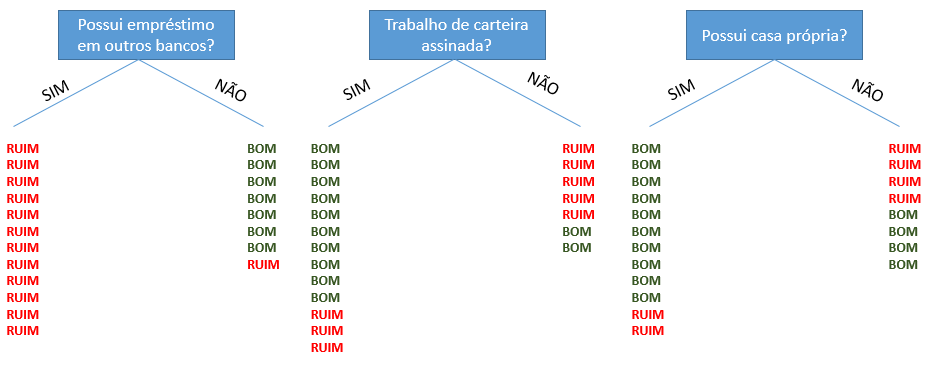
No diagrama, temos que dos 20 clientes da base do banco XYZ, dentre os que tomaram empréstimo em outros bancos, nenhum pagou a dívida. E dentre os que não tomaram, apenas um não pagou a dívida com o banco XYZ.

Com base na incerteza, podemos dizer que possuir empréstimo em outro banco é a melhor.

Veja que essa variável tem zero de incerteza, com base no histórico, todos os clientes que possuem empréstimo em outros bancos são maus pagadores.

E qual a pior variável?

Seguindo a mesma lógica, é a variável possui ou não casa própria. Veja que caso a pessoa não possua casa própria, a gente não consegue decidir se é mais provável que ela seja boa ou má pagadora. É equivalente a jogar uma moeda e decidir na sorte.

Criando variáveis dummy no SAS

Há algumas formas simples de criar uma variável dummy no SAS, vou demonstrar duas que eu utilizo constantemente.

Primeiramente, apenas para relembrar, uma variável dummy é um artifício criado para representar uma característica do indivíduo da amostra. Podemos criar uma variável dummy do sexo por exemplo, que receberá 1 se o indivíduo for mulher e 0 se for homem. Ou então criar uma dummy para reprovação, onde o aluno recebe 1 caso tenha sido reprovado e 0 caso tenha sido aprovado.

Isso serve para incluir informações não numéricas nas regressões, ou informações numéricas que não representam quantidades. Por exemplo, se eu tiver sala 1 e sala 2 de aula em uma regressão, qualquer operação aritmética com os números da sala não vai fazer sentido. Seria idêntico ter sala A e B.

No post Como calcular a diferença entre duas datas no SAS? criei a tabela turma_1. Vamos utilizá-la para criar duas novas variáveis, aprovacao_1 e aprovacao_2. Essas variáveis vão atribuir 1 ao aluno aprovado, no caso, a aprovação ocorre caso o aluno tenha nota maior ou igual a 6. Caso o aluno não tenha nota suficiente para aprovação, a dummy criada receberá 0:

data turma_1_1;
    set turma_1;
    aprovacao_1 = notas >= 6;
    if notas >= 6 then aprovacao_2 = 1;
    else aprovacao_2 = 0;
run;

Veja que com essa nova variável poderíamos fazer regressões para estudar o que afeta a reprovação de um aluno, ou até mesmo se a reprovação afeta algo.

Simples, não?

Qualquer dúvida, sugestão ou crítica é só comentar abaixo!

Reforçando o uso do R-quadrado: por que o autor usou um R-quadrado baixo?

Já falei sobre o R-quadrado no post Regressão Linear Simples – Parte 3. Ainda assim, o r-quadrado é uma medida que pode ter algumas pegadinhas.

Você verá em muitos artigos científicos os autores buscando algum efeito causal, rodando uma regressão e tirando alguma conclusão mesmo que no output da regressão tenha saído um r-quadrado baixo. Pode isso Arnaldo?

De forma rápida, a regra é clara, pode sim!

De forma mais demorada: O r-quadrado é uma medida de dependência linear entre as variáveis, ele vai te ajudar a entender o quanto seu modelo vai explicar a variável dependente. Você deve interpretá-lo como sendo o percentual da variação da variável resposta que é explicada por um modelo linear.

Você foi lá, fez seu experimento, aleatorização certinha, fez os testes legais, a variável independente tem lá um p-valor legalzinho na regressão, de forma intuitiva faz sentido a causalidade dela, mas chegou em um r-quadrado baixo. E aí, deu ruim?

Não, o r-quadrado vai te ajudar a encontrar um bom modelo, um modelo mais robusto em comparação com um modelo mais simples. Mas ele não vai anular o efeito causal que você obteve, por isso você vai sim encontrar regressões em diversos papers renomados explicando alguma causalidade utilizando regressões com baixo r-quadrado.

Para os que falam inglês, leia também: http://blog.minitab.com/blog/adventures-in-statistics/how-high-should-r-squared-be-in-regression-analysis

Você vai ouvir falar por aí: variáveis de controle

Muitas vezes quando você faz uma regressão, você quer saber quanto uma variável impacta a outra, por exemplo quanto um ano a mais de estudos impacta o salário. No entanto, outras variáveis podem afetar o salário, como profissão e até o sexo. Para saber como os anos de estudos impactam o salário, você precisa controlar as demais variáveis e isolar o efeito dos anos de estudos. Sendo assim, as variáveis profissão e sexo devem ser levadas em conta na sua análise, basicamente sendo inseridas na sua regressão. Isso são as variáveis de controle, são variáveis que possivelmente ou com certeza causam efeito na sua variável dependente, no nosso caso o salário, e que devem ser levadas em consideração para que a gente consiga estimar o efeito único de uma variável independente na variável dependente.