A função qqplot() do R – pertencente ao pacote ggplot2 – é uma das melhores para se fazer gráficos. Este post, sem muitas enrolações, é basicamente uma continuidade do Gráficos em R. Aqui vamos utilizar os dados da base Wage do pacote ISLR do R.
Para começar, apenas carregue os pacotes e visualize a base:
library(ggplot2); library(ISLR); View(Wage);
## Tracando grafico simples com qplot ## por default, temos um histograma bem simples qplot(wage, data=Wage);
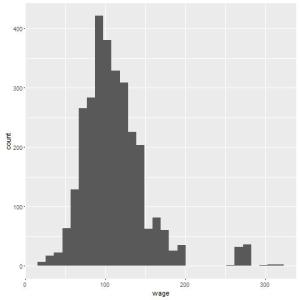
qplot(wage, data=Wage, bins=15);
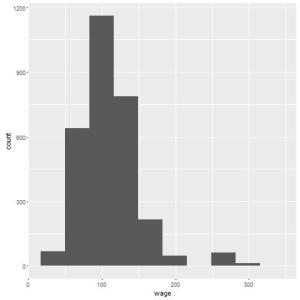
## Agora, vamos visualizar cada barra separando pelo estado civil qplot(wage, colour=maritl, data=Wage);
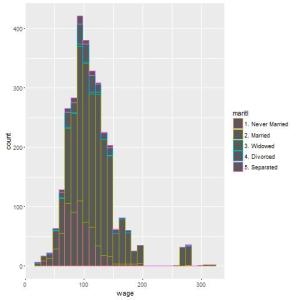
## Separar apenas com a cor do contorno nao ficou legal ## vamos trocar tambem a cor de preenchimento utilizando fill qplot(wage, colour=maritl, fill=maritl, data=Wage);
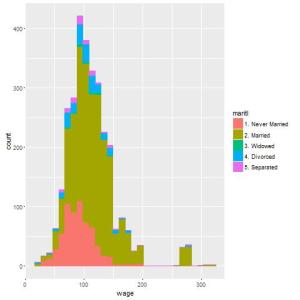
## Podemos inclusive preencher os blocos com cores diferentes ## Por exemplo, para cada estado civil, queremos ver quantos sao ## saudaveis e quantos nao sao qplot(wage, colour=maritl, fill=health, data=Wage);
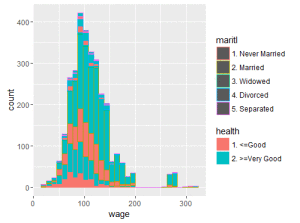
## Podemos visualizar graficos de densidade qplot(wage, colour=maritl, data=Wage, geom="density");
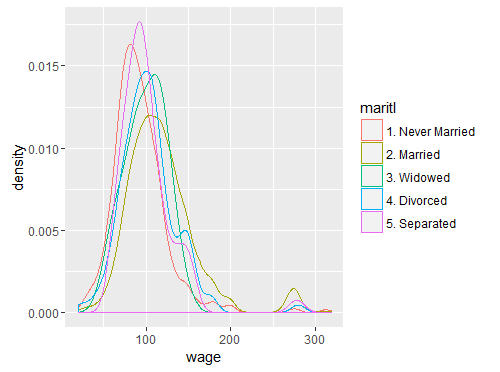
## Podemos tentar entender como duas variaveis interagem ## Exemplo: plotar salario vs idade qplot(wage, age, data=Wage);
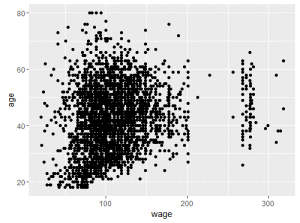
## Ou ate tentar ver alguma relacao nao linear qplot(wage, age*age, data=Wage);
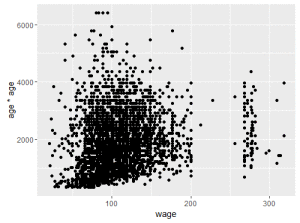
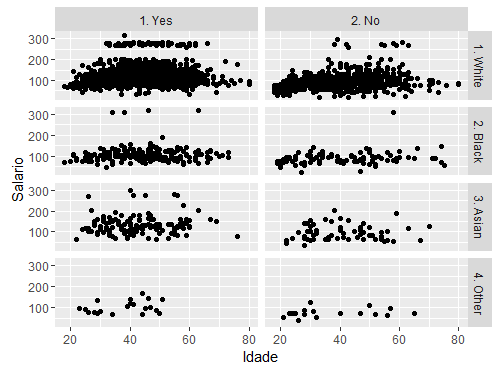
## Um pouco mais complexo, podemos verificar o comportamento de idade por salario ## para cada raca, dividindo ainda por pessoas que possuem ou nao plano de saude ## essa segunda divisao (raca por plano de saúde) eh feita utilizando facets qplot(age, wage, data=Wage, facets=race~health_ins, xlab="Idade", ylab="Salario");
## Por fim, podemos fazer um boxplot, mas divindo uma variavel por
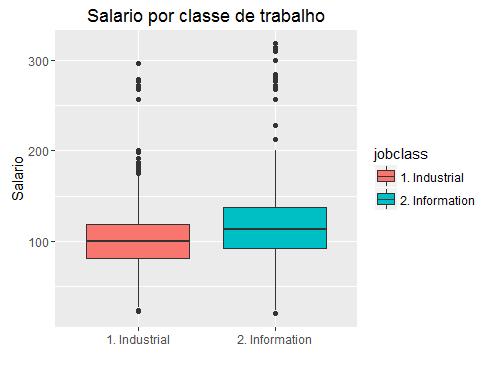
## cada uma das diferentes classes de uma outra (categorica)
## vamos observar o boxplot de salario para cada classe de trabalhador
## main indica o titulo do grafico, ylab o titulo do eixo y
qplot(jobclass, wage, data=Wage, geom=c("boxplot"),
fill=jobclass, main="Salario por classe de trabalho",
xlab="", ylab="Salario")
Agora você já está pronto para fazer diversos gráficos diferentes no R!



